
Myslím si, že Aaronova představa programování jako čarování je vlastně dost přesná. Čaroděj vytvoří kouzelnou větu v neznámém jazyce, neznámého významu, která se neznámo jak vykoná, aby nakonec dostal, co chtěl.
Ale přece každý jazyk je neznámý, dokud se nenaučíme slova a skladbu věty. A žádná věta nedává smysl, dokud se v jazyce nenaučíme vyjádřit své myšlenky. Zbývá pak už jediný rozdíl mezi čarodějem a neprogramátorem – kouzelná hůlka, která kouzelnou větu vykoná. A ani čaroděj většinou netuší, jak to ta hůlka provede.
Kdybych se někdy znovu učil programovat, chtěl bych začít s How to Design Programs (HTDP). Kouzelný jazyk, který HTDP používá, se jmenuje Racket a kouzelná hůlka je vývojové prostředí DrRacket.
Programovací jazyk Racket, a Scheme vůbec, má tu výhodu, že je syntakticky jednoduchý. To znamená, že jde jednoduše vysvětlit, jak vytvořit kouzelnou větu – začátek a konec je pevně daný, stejně jako kde je to co se má stát a kde je to s čím se to má stát.
To ale neubírá na síle programovacího jazyka! Jestliže Neprogramátor je úvod k HTDP, pak zkratka je Scheme Primer a základ R5RS. A pak je tu samozřejmě SICP.
Takže… cože to to programování vlastně je? Jakože čarovat? Můžu se to naučit? A jak?
Dialog s kouzelnou hůlkou představuje interaktivní způsob programování, Dopis pro kouzelnou hůlku vysvětluje práci programátorů a Nekonečně kouzelné jazykolamy pojednávají o tom, jak a proč toho programátoři tolik zvládnou. Kouzelné čtení a Čarodějnický žargon jsou pro doplnění.
Učíme se ve spirále a Neprogramátor aspiruje být první částí spirály k programování.
Jazyk čeština má deset druhů slov: podstatná
jména (třeba "kniha"), přídavná jména (třeba
"kouzelná"), zájmena, číslovky (třeba 0 a
3.14), slovesa (třeba
sečti a spoj), a pak ještě příslovce,
předložky, spojky, částice a citoslovce. Každá věta
začíná velkým písmenem, pak jsou slova oddělená mezerami, a nakonec
tečka ., vykřičník !, nebo otazník
?.
Sečti 0 a 3.14!Spoj "kouzelná" a "kniha".V jazyce čeština je stavba věty složitá, takže příklady vět zní kostrbatě a nejspíš by se řeklo spíše:
Prosím, sečti pro mě čísla nula a 3.14.Co vznikne, když ke slovu "kouzelná" přidáš slovo "kniha"?Kouzelný jazyk Racket má jen dva druhy slov: podstatná jména
a slovesa. Podstatná jména ukrývají nějakou informaci. Třeba
"kniha", "kouzelná", 0 a
3.14 jsou všechno podstatná jména kouzelného jazyka.
Slovesa říkají, co se má s podstatnými jmény stát. Třeba +
a string-append jsou slovesa kouzelného jazyka. Každá
kouzelná věta začíná závorkou ( a hned po ní následuje
sloveso. Potom jsou podstatná jména oddělená mezerami a úplně nakonec
zase závorka ).
(+ 0 3.14)(string-append "kouzelná" "kniha")Aby čaroděj mohl v kouzelném jazyce vyjádřit, co chce, kromě slov a skladby věty (odborně syntax) potřebuje znát i význam slov (odborně sémantika), protože i když slova zná a vytvoří kouzelnou větu podle správných pravidel, výsledek nemusí dávat smysl. Věta
Prosím, sečti pro mě nulu a "kniha".smysl nedává, stejně tak ani kouzelná věta
(+ 0 "kniha")A nakonec je tu kouzelná hůlka, která umí vykonat kouzelné věty zapsané v kouzelném jazyce Racket. Kouzelná hůlka vykoná kouzelnou větu
(+ 0 3.14)tak, že se z ní stane
3.14a z kouzelné věty
(string-append "kouzelná" "kniha")"kouzelnákniha"Když kouzelná hůlka vykoná kouzelnou větu, výsledek je slovo kouzelného jazyka. Může to být podstatné jméno ukrývající informaci, kterou chtěl čaroděj získat. Nebo to může být sloveso, které čaroděj použije pro další čarování.
Protože výsledek vykonání kouzelné věty je slovo kouzelného jazyka, může čaroděj použít více jednodušších vět, aby vytvořil jednu dlouhou mocnou kouzelnou větu.
(+ (+ 0 3.14) (+ 0 3.14))6.28Jenže aby se vykonala kouzelná věta složená z menších, musí se nejprve vykonat ty menší. O to se už ale postará kouzelná hůlka.
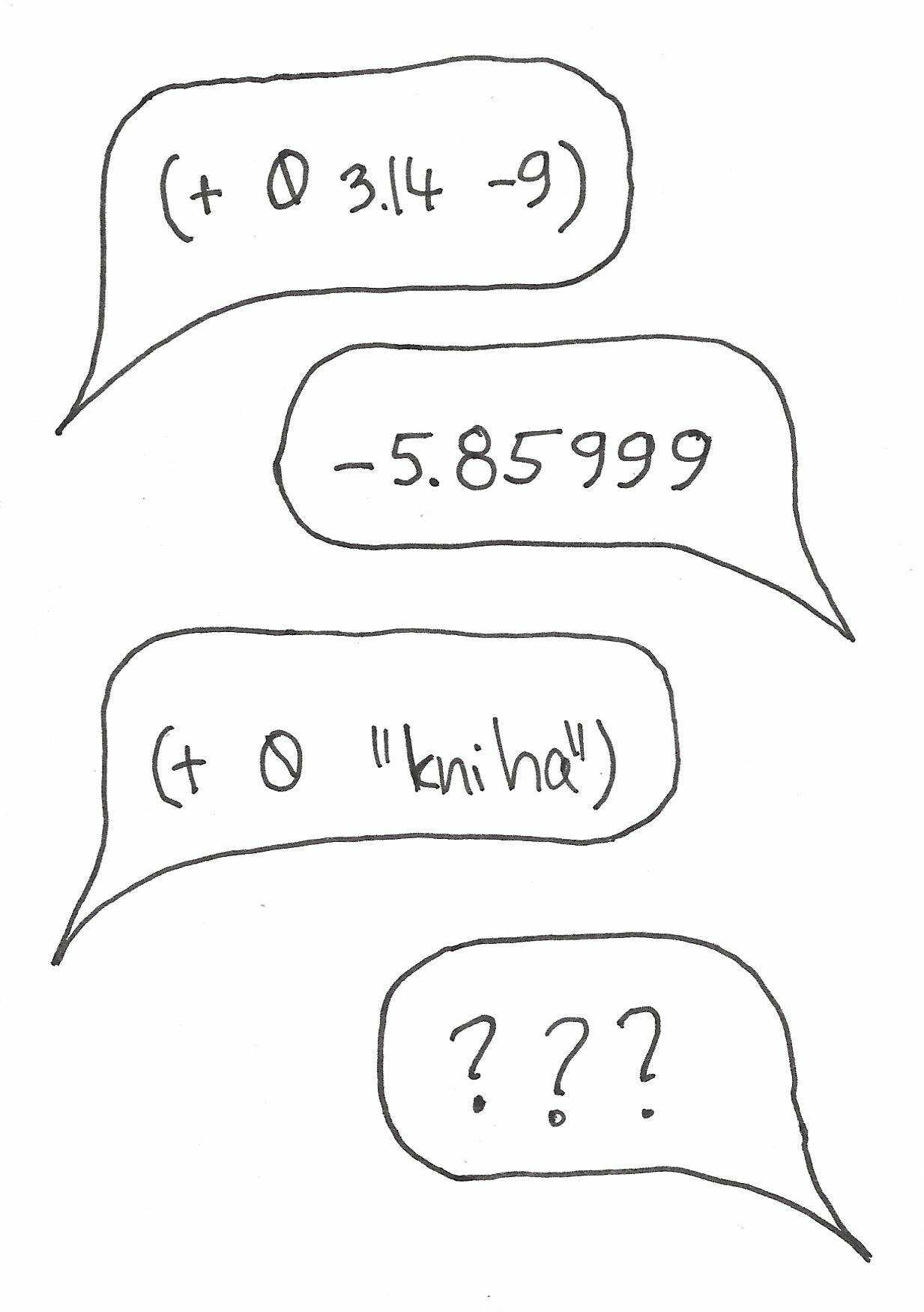
Kouzelná hůlka poslouchá, jestli po ní čaroděj něco nechce. Pokud ji čaroděj předá kouzelnou větu, kouzelná hůlka kouzelnou větu přečte a vykoná, vytiskne výsledek a pak čeká, až jí čaroděj předá nějakou další kouzelnou větu. Anglicky se Přečti, Vykonej, Vytiskni (výsledek), Opakuj řekne Read, Evaluate, Print, Loop, a tak se dialogu s kouzelnou hůlkou říká zkrátka REPL.
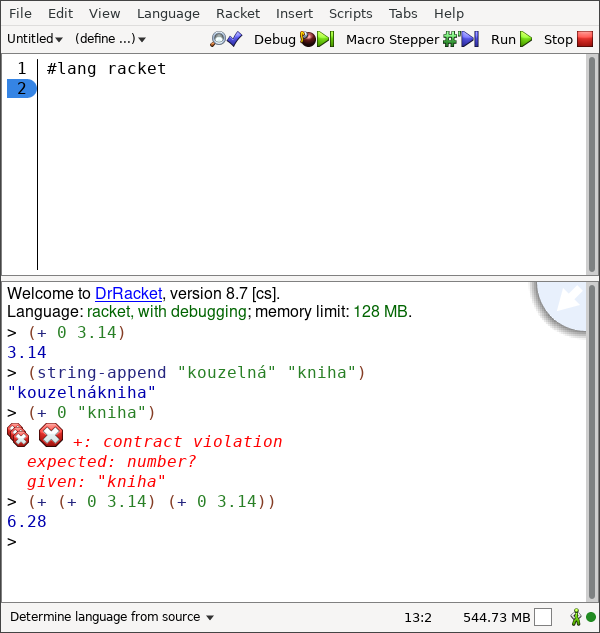
REPL je ve vývojovém prostředí DrRacket prostor v dolní polovině a použijeme jej pro sdílení kouzelných vět s kouzelnou hůlkou.
Podstatná jména kouzelného jazyka uchovávají nějakou informaci. Jsou ale různé typy informací – desetinná čísla, celá čísla, nebo text, či pravdivostní hodnota: pravda a nepravda. S každým typem podstatných jmen je potřeba zacházet trochu jinak, a tak se pro každý typ podstatného jména hodí trochu jiná slovesa.
Když se stejná informace, třeba číslo nebo text, používá na více místech, hodí se si ji zapamatovat. To se nejlépe udělá tak, že se informace pojmenuje a její jméno se pak použije všude tam, kde je informace třeba.
Když kouzelná hůlka vykoná kouzelnou větu, výsledkem je slovo kouzelného jazyka. A když je to slovo podstatné jméno a informace v něm ukrytá buď pravda, nebo nepravda, říká se, že ona kouzelná věta je predikát.
Čarodějové často tvoří mocné kouzelné věty, kde použijí predikát a dvě další kouzelné věty. Podle toho, jestli je predikát pravda nebo nepravda, vykoná kouzelná hůlka první nebo druhou z těch dvou dalších kouzelných vět. Takovým mocným kouzelným větám se říká podmínkový výraz a kouzelná hůlka tak čarodějům pomáhá s rozhodováním.
Čaroděj občas ví, jakou kouzelnou větu by chtěl s kouzelnou hůlkou sdílet – jaké by použil sloveso a co by se mělo stát s podstatnými jmény. Jenže kouzelná hůlka žádné takové sloveso nezná. Potom čaroději nezbývá, než kouzelnou hůlku nové kouzelné sloveso naučit. Musí ale použít jen slovesa a podstatná jména kouzelného jazyka, kterým kouzelná hůlka rozumí.
Začít jednoduchým příkladem je složité, protože jednoduché příklady nejsou žádné čáry. Sečíst první číslo s druhým je snadné, na to člověk nemusí být čaroděj. Jenže když se učíme nový jazyk, začínáme právě s jednoduchými slovy a jednoduchými větami. Kouzelný jazyk není výjimkou.
(+ 0 3.14)
je věta kouzelného jazyka, která sečte 0 a
3.14. Podstatná jména této kouzelné věty jsou čísla a čísla
se v kouzelném jazyce píší stejně. Slovesem této kouzelné věty je
+, symbol, který používáme v matematice.
Pro podstatná jména kouzelného jazyka, která uchovávají nějakou
číselnou informaci, se kromě kouzelného slovesa + hodí ještě
-, *, /, nebo min, max, a abs.
Neprogramátora občas trápí, jaký je obsah obdélníku, který je 10 cm
široký a 3 cm vysoký. Obsah obdélníku se vypočítá
šířka × výška, tedy 10 × 3 = 30
cm2.

Čaroděj se o svoje trápení podělí s kouzelnou hůlkou:
(* 10 3)Neprogramátor i čaroděj musí tedy vědět, co chce vypočítat a jak.
Třeba i obvod takového obdélníku; ten je
2 × (šířka + výška). Neprogramátor pak zapíše do kalkulačky
2 × (10 + 3) a kalkulačka mu vrátí výsledek 26
cm. Čaroděj místo toho napíše kouzelné hůlce do REPL:
(* 2 (+ 10 3))To je mocná kouzelná věta složená ze dvou. Výsledek vykonání té
vnitřní, (+ 10 3),
je podstatné jméno kouzelného jazyka 13. Kouzelná
hůlka tak z kouzelné věty (* 2 (+ 10 3))
udělá nejdříve (* 2 13)
a pak 26.
Nejdůležitější slovesa kouzelného jazyka pro práci s textem jsou:
string-length,
substring,
string-append,
number->string
a string->number.
Hodně kouzelných sloves připomíná angličtinu.
Jak dlouhé je slovo "Neprogramátor"?
Pokud se neprogramátor nepřehlédl, má 12 znaků. Čaroděj mezitím píše
kouzelné hůlce do REPL:
(string-length "Neprogramátor")A také celkem jednoduše nechá kouzelnou hůlku odpovědět celou větou,
protože string-append
slouží pro spojení textu:
(string-append "Délka slova Neprogramátor je "
(number->string (string-length "Neprogramátor")))Pro každý typ podstatného jména se hodí trochu jiná slovesa. Také se
očekává, že slovesa kouzelného jazyka se budou používat se správným
typem podstatných jmen. Byla by proto chyba použít pro sloveso string-append
podstatné jméno, které je výsledkem vykonání kouzelné věty (string-length "Neprogramátor"),
protože string-append
se hodí na text, jenže výsledek vykonání (string-length "Neprogramátor")
je číslo.
To ale neznamená, že slovesa kouzelného jazyka očekávají pořád stejný typ podstatných jmen, jako třeba v kouzelné větě o části textu:
(substring "Neprogramátor" 2 (string-length "Neprogramátor"))Kouzelné sloveso substring
očekává jako první podstatné jméno text. Jako druhé a třetí očekává ale
číslo – pozici, od které má text zkrátit, a pozici kam až. Pozor, pozice
začínají od nuly!
Podstatná jména #t a #f jsou
pravdivostní hodnoty. Pravda a nepravda. K těm se hodí slovesa and, or a not. Větami
kouzelného jazyka složených z takových podstatných jmen a sloves se
zabývá Logika.
Krátká anglická poznámka: Anglicky je pravda true a nepravda
false, proto #t a #f. V
angličtině znamená and spojku “a”, or znamená “nebo” a
not znamená “ne”.
Krátká logická poznámka: Lež není opak pravdy. Opakem pravdy je nepravda, zatímco lež je úmyslné uvedení v omyl.
Kouzelné větě začínající slovesem not se říká
negace. Taková kouzelná věta má jedno podstatné jméno. Pro
(not #t)
je výsledek vykonání #f, a naopak,
na kouzelnou větu (not #f)
odpoví kouzelná hůlka #t.

Kouzelná věta začínající slovesem and je
konjunkce a věta začínající or je
disjunkce. Obě mají kromě slovesa ještě dvě podstatná
jména.
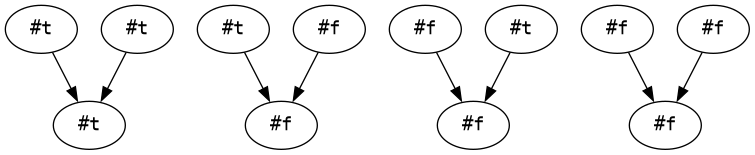
Kouzelná hůlka odpoví #t na kouzelnou
větu (and #t #t).
Na všechny ostatní kouzelné věty začínající kouzelným slovesem and, tedy (and #t #f),
(and #f #t)
a (and #f #f),
odpoví kouzelná hůlka #f.
Obdobně je to s kouzelným slovesem or – kouzelná
hůlka odpoví #f jen na
kouzelnou větu (or #f #f).
Na všechny ostatní, tedy (or #f #t),
(or #t #f)
a (or #t #t),
odpoví kouzelná hůlka #t.

Pravdivostní hodnoty jsou důležité při rozhodování; použijeme je v kapitole Vykonat či nevykonat: predikáty a podmínkové výrazy.
Podstatná jména:
0 nebo 3.14"Neprogramátor"#t a #fSlovesa pro čísla:
+
sečti čísla-
odečti čísla*
vynásob čísla/
vyděl číslamin
najdi nejmenší číslomax
najdi největší čísloabs
absolutní hodnota číslaSlovesa pro text:
string-length
počet znaků textusubstring část
textu od dostring-append
spojení textůnumber->string
číslo na textstring->number
text na čísloSlovesa pro pravdivostní hodnoty:
and
konjunkceor
disjunkcenot
negaceStejně jako se čaroděj může naučit nová slova kouzelného jazyka, může se nová slova naučit i kouzelná hůlka. Tedy je to spíše čaroděj, kdo kouzelnou hůlku nová slova naučí. Když použije ty správné kouzelné věty.
Kouzelná věta začínající slovesem let může
přispět k přehlednosti při obdélníkových počtech i hledání délky
slova.

Obsah obdélníku se vypočítá šířka × výška. Kouzelné
sloveso let použijeme v
kouzelné větě, ve které pojmenujeme číselnou informaci ukrytou v
kouzelných podstatných jménech 10 a 3:
(let ((šířka 10)
(výška 3))
(* šířka výška))Obvod je 2 × (šířka + výška) a kouzelné hůlce píšeme do
REPL:
(let ((šířka 10)
(výška 3))
(* 2 (+ šířka výška)))Čaroděj může pojmenovat i podstatná jména typu text:
(let ((slovo "Neprogramátor"))
(string-append "Délka slova " slovo " je "
(number->string (string-length slovo))))Navíc čaroději nic nebrání použít výsledek vykonání kouzelné věty
začínající kouzelným slovesem let jako část
jiné kouzelné věty:
(let ((slovo "Neprogramátor"))
(let ((část (substring slovo 2 (string-length slovo))))
(string-append "Délka slova " část " je "
(number->string (string-length část)))))Pomocí let lze
pojmenovat podstatná jména, která na sobě nezávisí. Jenže podstatné
jméno část závisí na podstatném
jméně slovo. Místo let je tak
potřeba použít let*. let* je sloveso
kouzelného jazyka, které je hodně podobné let, jen o
trochu lépe umí pojmenovat více věcí najednou – následující slova,
například část, mohou záviset na
těch předchozích, v tomto případě na slovo:
(let* ((slovo "Neprogramátor")
(část (substring slovo 2 (string-length slovo))))
(string-append "Délka slova " část " je "
(number->string (string-length část))))Když čaroděj řekne kouzelné hůlce:
(let ((šířka 10)
(výška 3))
(* šířka výška))kouzelná hůlka odpoví 30. Když se
hned na to čaroděj zeptá:
šířkakouzelná hůlka neví. Čaroděj naučil kouzelnou hůlku nová slova jen na chvilku.
Aby si kouzelná hůlka nová slova zapamatovala, vysvětlí je čaroděj v
kouzelných větách začínajících slovesem define:
(define šířka 10)
(define výška 3)Kouzelná hůlka pak už ví a na šířka odpoví 10, na výška odpoví 3 a na (* šířka výška)
odpoví 30. A na (* 2 (+ šířka výška))
samozřejmě 26.
Slovesa let a let* slouží
čaroději pro dočasné pojmenování informací v jedné větě.
Slovesem define čaroděj
naučí kouzelnou hůlku novou informaci, kterou si kouzelná hůlka
zapamatuje.
Čaroděj může kouzelnou hůlku připravit na různé situace. To udělá
tak, že pro každou situaci, která může nastat, vymyslí kouzelné slovo.
Nebo kouzelnou větu. A pak vymyslí kouzelné slovo či větu pro tu samou
situaci, když nenastane. K tomu čaroděj použije kouzelné sloveso if:
(if prší?
"je mokro"
"neprší")Krátká anglická poznámka: Z angličtiny se if přeloží jako “když”.
Pojmenování informací: definice proměnných už tu bylo, takže můžeme napsat kouzelné hůlce do REPL:
(let ((prší? #t))
(if prší?
"je mokro"
"neprší"))a taky
(let ((prší? #f))
(if prší?
"je mokro"
"neprší"))Kouzelné větě začínající kouzelným slovesem if se říká
podmínkový výraz. Výsledek vykonání podmínkového výrazu záleží
na pravdivostní hodnotě prvního podstatného jména, kterému se říká
predikát. (Výsledek vykonání predikátu je vždy #t nebo #f.) Dohoda je,
že predikáty končí otazníkem (?), ale neplatí
to vždy. A protože kouzelné věty lze vnořovat a vytvářet tak mocné
kouzelné věty, může být namísto prvního podstatného jména nějaká
kouzelná věta; v takovém případě končí otazníkem sloveso.
No a aby se čarodějové neztratili v množství situací, na které kouzelnou hůlku připravují, kreslí si obrázky, kterým říkají vývojové diagramy nebo rozhodovací stromy.
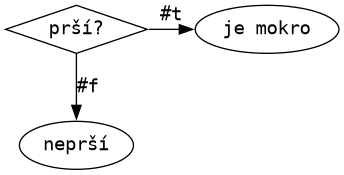
Čarodějům se vžycky nakonec podaří všechny situace popsat predikáty,
tedy kouzelnými slovy či kouzelnými větami, na které kouzelná hůlka
odpoví vždy jen #t nebo #f.

Třeba obdélník může být nakreslený “na šířku”, jako na obrázku. Když není nakreslený “na šířku”, tak může být nakreslený “na výšku”. A když není ani “na výšku”, není to obdélník!
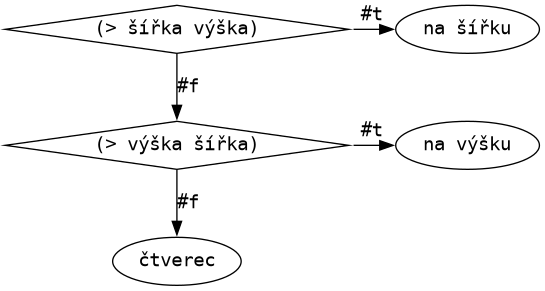
Kouzelné věty můžeme vnořovat a tvořit tak mocné kouzelné věty:
(let ((šířka 10)
(výška 3))
(if (> šířka výška)
"na šířku"
(if (> výška šířka)
"na výšku"
"čtverec")))Pokud je možných situací opravdu hodně, není vnořování vždy
přehledné. V takových případech čarodějům místo if poslouží
cond:
(let ((šířka 10)
(výška 3))
(cond
((> šířka výška) "na šířku")
((> výška šířka) "na výšku")
(else "čtverec")))Za kouzelným slovesem cond následují
kouzelné skoro-věty. Skoro- proto, že na místě, kde je v kouzelné větě
sloveso, je v kouzelné skoro-větě predikát. Za predikátem už následuje
kouzelné podstatné jméno nebo kouzelná věta, kterou má kouzelná hůlka
vykonat, když situace nastane (výsledek vykonání predikátu je #t). Každá z
kouzelných skoro-vět následujících po cond tak
kouzelné hůlce říká: “Jestli na moje první slovo nebo větu odpovíš #t, vykonej ty
další! To je výsledek!”
Kouzelné slovo else je vlastně
#t a v
kouzelné skoro-větě tedy říká: “Vždy vykonej co je za mnou!” else se hodí,
když čaroděj ví, co má kouzelná hůlka udělat, pokud všechny ostatní
situace nenastaly (výsledky vykonání predikátů jsou #f).
Kouzelným větám začínajícím kouzelnými slovesy if a cond se říká
podmínkové výrazy – jejich vykonávání je podmíněné predikátem.
Konvence pro predikáty je, že končí otazníkem (?); pro
kouzelná slovesa použitá v predikátech pro čísla to ale většinou
neplatí:
=
všechna čísla jsou si rovna?<
všechna čísla řazena vzestupně?>
všechna čísla řazena sestupně?<=
všechna čísla řazena neklesajíce?>=
všechna čísla řazena nestoupajíce?I když pro některá ano:
number? je
číslo?integer? je
celé číslo?zero?
je nula?positive? je
kladné?negative? je
záporné?odd?
je liché?even?
je sudé?Kouzelná slovesa pro text, která se používají v predikátech, konvenci s otazníkem na konci dodržují:
string? je
text?string=? jsou
texty stejné?string-ci=?
jsou texty stejné bez ohledu na velikost písmen?string<?,
string>?,
string<=?,
string>=?
jsou texty lexikograficky řazené?string-ci<?,
string-ci>?,
string-ci<=?,
string-ci>=?
jsou texty lexikograficky řazené bez ohledu na velikost písmen?A kouzelná slovesa pro pravdivostní hodnoty jsou tři, všechna bez otazníku:
and
konjunkceor
disjunkcenot
negaceČaroděj vymýšlí kouzelné věty, které kouzelné hůlce píše do REPL. Kouzelná hůlka kouzelné věty vykoná a čaroději napíše zpátky výsledek. Často se ale stane, že čaroděj napíše – nebo chce napsat – kouzelnou větu, kterou kouzelná hůlka nechápe. Protože čaroděj použil kouzelná slova, která kouzelná hůlka nezná.
Jak na nová kouzelná podstatná jména víme z Pojmenování informací: definice proměnných; s novými kouzelnými slovesy je to podobně.

Obsah obdélníku se vypočítá šířka × výška a čaroděj tak
píše kouzelné hůlce:
(* 10 3)Raději by ale psal:
(obsah 10 3)To aby bylo jasné, co po kouzelné hůlce chce.
Čaroděj tedy kouzelné hůlce vysvětlí, jak nová kouzelná věta vypadá – jakým slovesem začíná a jaká podstatná jména následují. Vysvětlí jí také význam nové kouzelné věty – co se s podstatnými jmény v nové kouzelné větě má stát.
Stejně jako pro nová podstatná jména, použije čaroděj pro nová
slovesa (a tedy pro nové kouzelné věty) kouzelnou větu začínající
kouzelným slovesem define:
(define (obsah šířka výška)
(* šířka výška))Tentokrát ale po define
následuje nová kouzelná věta, jak by ji chtěl čaroděj kouzelné hůlce
napsat, a hned potom její význam, tedy co nová kouzelná věta
znamená.
Takové kouzelné větě se říká definice funkce obsah s parametry šířka a výška. Podstatným jménům v nové kouzelné větě se říká parametry. Významu, který následuje, se říká implementace funkce.
Pak už kouzelná hůlka odpoví i na kouzelnou větu:
(obsah 10 3)Takové kouzelné větě se říká volání funkce obsah s argumenty 10 a 3, nebo aplikace funkce obsah na argumenty 10 a 3. Argumenty jako aktuální hodnoty.
Stejným způsobem naučí čaroděj kouzelnou hůlku i kouzelné sloveso
obvod:
(define (obvod šířka výška)
(* 2 (+ šířka výška)))A pak se kouzelné hůlky zeptá na:
(obvod 10 3)(define (obsah šířka výška)
(* šířka výška))
(define (obvod šířka výška)
(* 2 (+ šířka výška)))
(define (obdélník šířka výška)
(let ((orientován (cond
((> šířka výška) "na šířku")
((> výška šířka) "na výšku")
(else "čtverec")))
(text-obsah (number->string (obsah šířka výška)))
(text-obvod (number->string (obvod šířka výška))))
(string-append "Obdélník "
(number->string šířka)
" x "
(number->string výška)
" je " orientován "."
" Jeho obsah je " text-obsah
" a obvod " text-obvod ".")))
(obdélník 10 3)
(obdélník 3 10)
(obdélník 4 4)Kouzelné sloveso define může
čaroděj použít k tomu, aby kouzelnou hůlku naučil nové kouzelné sloveso.
To udělá tak, že napíše, jak by nová kouzelná věta (používající nové
kouzelné sloveso) měla vypadat a co by se mělo stát s podstatnými jmény
použitými v nové kouzelné větě:
(define (nové-kouzelné-sloveso podstatná-jména oddělená mezerami)
(co-vykonat-s podstatná-jména oddělená mezerami))Kde kouzelné sloveso co-vykonat-s musí kouzelná hůlka znát
předem.
Máme za sebou čtyři kapitoly popisující základy kouzelného jazyka: jaká jsou podstatná jména a která slovesa se k nim hodí, jak pojmenovat konkrétní informace ukryté v podstatných jménech, rozhodování ponechané na kouzelné hůlce a jak kouzelnou hůlku naučit nová kouzelná slovesa.
Nedá se říci, že neprogramátor je teď čaroděj. Ještě chvíli potrvá, než dokáže v kouzelném jazyce plynule vyjádřit své myšlenky, než přijde na to, jaké myšlenky to vlastně mají být, než se naučí čarodějnické triky ověřené staršími generacemi, jak zaznamenat a zkontrolovat kouzelné věty a jak spolupracovat s ostatními čaroději.
Neprogramátor by ale měl už vědět, cože to to programování-čarování vlastně je – že je to vytváření kouzelných vět, které vykoná kouzelná hůlka – a měl by umět přečíst a rozumět jednoduchým větám kouzelného jazyka.

Jazyk je jeden ze způsobů, jak se dají sdílet myšlenky. Použije se při mluvení a poslouchání a psaní a čtení. To, že kouzelná hůlka dokáže vykonat věty zapsané v některém z jazyků, neovlivňuje možnost sdílet v jazyce myšlenky. Vykonávání kouzelných vět kouzelnou hůlkou ale souvisí s tím, jak se dá s myšlenkami vyjádřenými v kouzelném jazyce pracovat, protože dost práce udělá právě kouzelná hůlka.
Jen pro připomenutí – kouzelný jazyk Racket má dva druhy
slov: podstatná jména a slovesa. Podstatná jména ukrývají nějakou
informaci. Třeba "kniha",
"kouzelná",
0 a 3.14 jsou
podstatná jména kouzelného jazyka. Slovesa říkají, co se má s
podstatnými jmény stát. Třeba + a string-append
jsou slovesa kouzelného jazyka. Každá kouzelná věta začíná závorkou
( a hned po ní následuje sloveso.
Potom jsou podstatná jména oddělená mezerami a úplně nakonec zase
závorka ).
A teď už několik myšlenek o nekouzelném světě zapsaných ve větách kouzelného jazyka.
(define (Pythagorova-věta a b c) ; a, b jsou odvěsny, c přepona
(= (* c c) (+ (* a a) (* b b))))
(define (vypočítej-přeponu-pro-odvěsny a b)
(sqrt (+ (* a a) (* b b))))
(define (vypočítej-odvěsnu-pro-přeponu-a-odvěsnu c a)
(sqrt (- (* c c) (* a a))))(define (oxidační-číslo->koncovka oxidační-číslo)
(cond ((= 1 oxidační-číslo) "-ný")
((= 2 oxidační-číslo) "-natý")
((= 3 oxidační-číslo) "-itý")
((= 4 oxidační-číslo) "-ičitý")
((= 5 oxidační-číslo) "-ičný, -ečný")
((= 6 oxidační-číslo) "-ový")
((= 7 oxidační-číslo) "-istý")
((= 8 oxidační-číslo) "-ičelý")))(define pravda #t)
(define (je-pravda? co)
(and pravda co))
(define (neplatí-že co)
(if (je-pravda? co)
(not pravda)
pravda))
(define (nepravda? co)
(neplatí-že (je-pravda? co)))
; Implikace, viz https://cs.wikipedia.org/wiki/Implikace
(define (když první-věta druhá-věta)
(cond
((and (nepravda? první-věta) (nepravda? druhá-věta))
pravda)
((and (nepravda? první-věta) (je-pravda? druhá-věta))
pravda)
((and (je-pravda? první-věta) (nepravda? druhá-věta))
(neplatí-že pravda))
((and (je-pravda? první-věta) (je-pravda? druhá-věta))
pravda))); Když prší, je mokro.
(define prší pravda)
(define je-mokro pravda)
; Možné negace věty 'Když prší, je mokro.'
(define když-neprší-je-mokro
(když (neplatí-že prší) je-mokro))
(define když-prší-není-mokro
(když prší (neplatí-že je-mokro)))
(define když-neprší-není-mokro
(když (neplatí-že prší) (neplatí-že je-mokro)))
; Jaká je negace věty 'Když prší, je mokro.'?
(equal? (neplatí-že (když prší je-mokro))
když-neprší-je-mokro)
(equal? (neplatí-že (když prší je-mokro))
když-prší-není-mokro)
(equal? (neplatí-že (když prší je-mokro))
když-neprší-není-mokro)Kouzelných (programovacích) jazyků je hodně (moc velká spousta). Pro zajímavost je tu řešení jednoduchého problému v osmi různých kouzelných jazycích.
Řešení problému v různých kouzelných jazycích obsahují příklady toho, jak pojmenovat podstatná jména, jak funguje rozhodování a jak tvořit nová kouzelná slovesa. Příklady řešení slouží jako ukázky skladby vět různých kouzelných jazyků a v tuhle chvíli není důležité jim rozumět, jen se na chvilku potrápit nad možným významem.
Podstatné jméno (číslo) 20 je pojmenované jako
dvaceta nové kouzelné slovesovětší-nežpracuje s jedním podstatným jménem (parametrem)číslo: jestli ječíslovětší neždvacet, kouzelné slovesovětší-nežvrátí nové podstatné jméno (text)"Větší je číslo.", kdečíslov textu je nahrazené konkrétní aktuální hodnotou; jinak vrátí"Větší je 20.".Pro otestování kouzelného slovesa
větší-nežse použijí podstatná jména (čísla, argumenty) 11 a 27.
Řešení v kouzelném jazyce Racket (nebo Scheme) se dá spustit pomocí kouzelné hůlky DrRacket.
; Je větší 20 nebo číslo?
(define dvacet 20)
(define (větší-než číslo)
(if (> číslo dvacet)
(string-append "Větší je " (number->string číslo) ".")
(string-append "Větší je " (number->string dvacet) ".")))
(větší-než 11)
(větší-než 27)Kouzelnou hůlkou pro kouzelný jazyk JavaScript je webový prohlížeč. Třeba ve Firefox stačí zmáčknout F12, přepnout na záložku “Konzole” a vést dialog s kouzelnou hůlkou. Většinou jsou ale věty kouzelného jazyka JavaScript součástí webových stránek.
// Je větší 20 nebo číslo?
var dvacet = 20;
function větší_než(číslo) {
if (číslo > dvacet)
return "Větší je " + číslo + ".";
else
return "Větší je " + dvacet + ".";
}
větší_než(11);
větší_než(27);Kouzelný jazyk Python vede v průzkumech o nejpopulárnější a nejjednodušší programovací jazyky.
# Je větší 20 nebo číslo?
dvacet = 20
def větší_než(číslo):
if číslo > dvacet:
print(f"Větší je {číslo}.")
else:
print(f"Větší je {dvacet}.")
větší_než(11)
větší_než(27)Některé kouzelné hůlky umí jen přečíst dopis a nelze s nimi vést dialog. Třeba kouzelný jazyk C je případ kouzelného jazyka, pro který existuje spoustu (hodně moc) kouzelných hůlek, ale jen s málokterou se dá vést dialog. Kouzelný jazyk C je legendární a je v něm napsáno hodně operačních systémů – programů, které jsou potřeba, aby se zařízení jako počítač dalo vůbec spustit.
/* Je větší 20 nebo číslo? */
#include <stdio.h>
#include <stdlib.h>
int const dvacet = 20;
char *
vetsi_nez(int const cislo)
{
char *str = (char *)malloc(100 * sizeof(char));
if (NULL == str) {
exit(1);
}
if (cislo > dvacet) {
sprintf(str, "Větší je %d.", cislo);
} else {
sprintf(str, "Větší je %d.", dvacet);
}
return str;
}int
main()
{
char *str;
str = vetsi_nez(11);
printf("%s\n", str);
str = vetsi_nez(27);
printf("%s\n", str);
free(str);
str = NULL;
return 0;
}Podobně legendární je i kouzelný jazyk Shell. Shellů je spoustu (hodně) a mezi nejznámější patří POSIX Shell a Bash. Shell souvisí s příkazovou řádkou operačního systému – když v Linux zapneme příkazovou řádku, ve většině případů tak začínáme s počítačem komunikovat v kouzelném jazyce Bash.
#!/bin/sh
dvacet=20
vetsi_nez()
{
if [ $1 -gt $dvacet ]
then
echo "Větší je $1."
else
echo "Větší je $dvacet."
fi
}
vetsi_nez 11
vetsi_nez 27Historie kouzelných jazyků je pestrá a každý kouzelný jazyk je v něčem jedinečný. Stejně tak i čarodějové jsou různí a každý čaroděj má své oblíbené kouzelné jazyky. Třeba kouzelný jazyk Forth.
\ Je větší 20 nebo číslo?
: dvacet 20 ;
: větší-než
dup dvacet >
if
else drop dvacet
then ." Větší je " . ." ." ;
11 větší-než
27 větší-nežKouzelný jazyk Uiua je velmi kompaktní. Nejen takové kouzelné jazyky existují.
# Je větší 20 nebo číslo?
Dvacet ← 20
VětšíNež ← $"Větší je _." ⨬(Dvacet◌)(∘) > Dvacet .
VětšíNež 11
VětšíNež 27Kouzelné jazyky jsou univerzální nebo specializované, na některé věci se hodí více, na některé méně. Třeba na logiku je skvělý kouzelný jazyk Prolog.
% Je větší 20 nebo číslo?
dvacet(D) :- D is 20.
vetsiNez(X) :- dvacet(D), X > D, format("Větší je ~d.", X).
vetsiNez(X) :- dvacet(D), X < D, format("Větší je ~d.", D).
vetsiNez(11).
vetsiNez(27).Je třeba si uvědomit, že příklady řešení jsou skutečně jen příklady řešení – jednoduchý problém lze ve stejném kouzelném jazyce vyřešit více způsoby, stejně jako třeba v češtině jde jednu informaci říci různě.

Povídat si s kouzelnou hůlkou má své kouzlo. Mnohdy ale vyjde lépe nechat kouzelnou hůlku naráz vykonat vše, co čaroděj chce.
Čaroděj často přemýšlí, ptá se kouzelné hůlky a dělá si poznámky – dokud nemá sepsáno vše, co chce vykonat. Nakonec předá kouzelné hůlce všechny kouzelné věty najednou a kouzelná hůlka je všechny, jednu po druhé, vykoná.
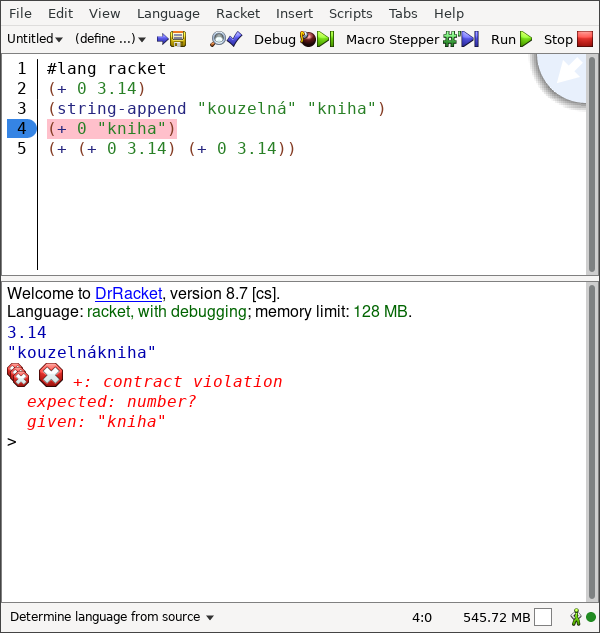
K psaní dopisu ve vývojovém prostředí DrRacket slouží horní polovina a kouzelná hůlka na dopis odpoví do REPL (dole).
Čarodějnické řemeslo je o vynalézání a psaní. Vynalézání většinou znamená hledání řešení problému. Mnohdy je vynalézání ale také hledání problému, a hlavně hledání dobrého popisu problému. V každém případě je k vynalézání potřeba znalost, která nesouvisí s programováním. Často je to matematika a fyzika, ale pokud je zadání problému vyhrát šachy, je nutné znát pravidla šachu.
A pak je tu psaní. Stejně jako knihy, programy se jednou napíšou a mnohokrát čtou. Vyplatí se proto napsat je dobře. Hezky. Takže čarodějové jsou vlastně spisovatelé.
Čarodějové pomáhají s řešením problémů ostatním, co čarovat neumí. Pomocí dopisů a kouzelné hůlky vytváří kouzelné lektvary, které stačí vypít. Samozřejmě je ale rozumné pít lektvary jen od důvěryhodných čarodějů.
K psaní dopisu pro kouzelnou hůlku používá čaroděj program pro psaní textu. Většinou je trochu vylepšený, takže dokáže zvýraznit kouzelná slova kouzelného jazyka a často je v něm i kouzelná hůlka. Takovému programu, kterým je třeba i DrRacket, se říká vývojové prostředí.
Práce čaroděje je napsat hezký dopis, ve kterém kouzelné hůlce vysvětlí, jak vyřešit nějaký problém. Kouzelná hůlka krásu dopisu neocení, ale čarodějové a čarodějky pracující na podobných problémech jistě ano. Kouzelnému dopisu se říká zdrojový kód.
Když chce čaroděj sdílet své řešení s ostatními, jednoduše pošle svůj
dopis pro kouzelnou hůlku i jim. Jako autor dopisu určí podmínky, za
kterých jej ostatní mohou použít; podmínky většinou sepíše do souboru
LICENSE.
Ostatním čarodějům a čarodějkám se také hodí vědět, jaký problém se
vlastně řeší a proč. K tomu slouží dobrá jména kouzelných sloves a
kouzelných podstatných jmen a také doplňující text,
dokumentace. Základním kamenem dokumentace je soubor
README.
A nakonec – občas se také hodí vědět, jak dopis pro kouzelnou hůlku vznikl. Nejznámější program, který se na průběžné sledování změn v dopisu pro kouzelnou hůlku používá, je Git.
Dopis pro kouzelnou hůlku napíšeme v DrRacket a uložíme do souboru v
adresáři (občas někdo adresáři říká složka). V tomhle adresáři pak
použijeme příkaz git, který nám se sledováním změn v dopisu
pro kouzelnou hůlku pomůže. Adresáři, ve kterém se příkaz
git použije, se říká repozitář.
DrRacket je vývojové prostředí pro psaní zdrojových kódu v programovacím jazyce Racket.
Git je program, který slouží ke sledování historie změn v adresáři se zdrojovým kódem. Adresáři se říká repozitář.
Kombinace DrRacket a Git se s výhodou použije pro zaznamenání vývoje řešení problému.
Příklad problému může být:
Podstatné jméno (číslo) 20 je pojmenované jako
dvaceta nové kouzelné slovesovětší-nežpracuje s jedním podstatným jménem (parametrem)číslo: jestli ječíslovětší neždvacet, kouzelné slovesovětší-nežvrátí nové podstatné jméno (text)"Větší je číslo.", kdečíslov textu je nahrazené konkrétní aktuální hodnotou; jinak vrátí"Větší je 20.".Pro otestování kouzelného slovesa
větší-nežse použijí podstatná jména (čísla, argumenty) 11 a 27.
Řešením třeba:
#lang racket
; Je větší 20 nebo číslo?
(define dvacet 20)
(define (větší-než číslo)
(if (> číslo dvacet)
(string-append "Větší je " (number->string číslo) ".")
(string-append "Větší je " (number->string dvacet) ".")))
(větší-než 11)
(větší-než 27)Protože dopis pro kouzelnou hůlku píšeme v DrRacket, je potřeba, aby
první řádek byl #lang racket.
Kouzelnou hůlku poprosíme o vykonání kouzelného dopisu klávesovou
zkratkou Ctrl + R nebo z menu Racket -> Run.
Výsledek je potom:
"Větší je 20."
"Větší je 27."A postup řešení:
$ git log
commit 591957744b7356c3169d86738c3b69f28d7e3dec (HEAD -> master, origin/master)
Author: Jméno Čaroděje <email@carodeje.xyz>
Date: Wed Jun 18 19:48:20 2025 +0200
Přidej řešení "Je větší 20 nebo číslo?"
commit 4535b310762c1cb4891e64af0b71368cd4cf8b4c
Author: Jméno Čaroděje <email@carodeje.xyz>
Date: Wed Jun 18 19:47:38 2025 +0200
Přidej licenci a readme$ git logZnak $ na začátku výpisu znamená, že následuje příkaz,
který čaroděj napíše do příkazové řádky. Příkazová řádka není REPL, ale souvisí s operačním systémem (třeba Windows
nebo Linux), který čaroděj používá.
Příkaz git log zobrazí historii repozitáře. Další
příkazy programu Git dokáží historii repozitáře zobrazit kompaktněji
nebo naopak detailněji.
commit 591957744b7356c3169d86738c3b69f28d7e3dec (HEAD -> master, origin/master)Řádek začínající commit jednoznačně identifikuje změnu v
dopisu pro kouzelnou hůlku. To, co následuje za commit, je
identifikátor změny. Poslední, HEAD a master v
závorce, jsou alternativní identifikátory dané změny.
Author: Jméno Čaroděje <email@carodeje.xyz>Na řádku je vidět, kdo změnu v dopisu provedl,
Date: Wed Jun 18 19:48:20 2025 +0200kdy ji zaznamenal do historie
Přidej řešení "Je větší 20 nebo číslo?"a co změna přínáší.
commit 4535b310762c1cb4891e64af0b71368cd4cf8b4c
Author: Jméno Čaroděje <email@carodeje.xyz>
Date: Wed Jun 18 19:47:38 2025 +0200
Přidej licenci a readmeTohle je druhá změna z výpisu příkazu git log. Vlastně
je to první zaznamenaná změna v repozitáři, protože git log
zobrazuje změny od nejnovější (nahoře) po nejstarší (dole). Z výpisu je
vidět, že v historii repozitáře jsou zaznamenány dvě změny.
Pro použití Git je potřeba Git stáhnout, nainstalovat a
nastavit. Po instalaci jde Git spustit: v Linux příkazem
git v příkazové řádce, ve Windows pak v příkazové řádce
programu Git Bash. Pro používání příkazu git je
potřeba:
Nastavit jméno čaroděje:
$ git config --global user.name "Jméno Čaroděje"Nastavit email čaroděje:
$ git config --global user.email "email@carodeje.xyz"Nastavit textový editor pro Windows:
$ git config --global core.editor "notepad"a pro Linux třeba:
$ git config --global core.editor "gedit"Repozitář je adresář, ve kterém je soubor s dopisem pro kouzelnou
hůlku. Vytvoří se stejným způsobem, jakým se adresáře a soubory vytváří
obvykle. Nebo přímo z DrRacket klávesovovou zkratkou Ctrl + S,
případně z menu File -> Save Definitions. Na vhodném místě
pak vytvoříme adresář vetsi-nez a v něm soubor
vetsi-nez.rkt. Obsah souboru je řešení problému. Dopis pro
kouzelnou hůlku. Zdrojový kód.
Druhý krok k vytvoření repozitáře je příkaz git init.
Když je Git nastavený a adresář vetsi-nez vytvořený, je
třeba se do adresáře vetsi-nez přepnout (v Linux
cd vetsi-nez, ve Windows kliknout pravým tlačítkem na
adresář vetsi-nez a vybrat Spustit Git Bash zde
…). A konečně v adresáři vetsi-nez napsat příkaz
git init a zmáčknout klávesu [Enter]:
$ git init
hint: Using 'master' as the name for the initial branch. This default branch name
hint: is subject to change. To configure the initial branch name to use in all
hint: of your new repositories, which will suppress this warning, call:
hint:
hint: git config --global init.defaultBranch <name>
hint:
hint: Names commonly chosen instead of 'master' are 'main', 'trunk' and
hint: 'development'. The just-created branch can be renamed via this command:
hint:
hint: git branch -m <name>
Initialized empty Git repository in /cesta/k/vetsi-nez/.git/Příkazy programu Git vždy souvisí s repozitářem a jsou tak spouštěny
z odpovídajícího adresáře. Takže třeba pro repozitář
vetsi-nez je příkaz
$ git status
On branch master
No commits yet
Untracked files:
(use "git add <file>..." to include in what will be committed)
vetsi-nez.rkt
nothing added to commit but untracked files present (use "git add" to track)spouštěn (v příkazové řádce) z adresáře vetsi-nez.
Příkaz git status zobrazí stav repozitáře a ve výpisu je
vidět, že v adresáři je nový soubor, který ještě není v historii
repozitáře zaznamenán.
Jako první se do repozitáře přidávají soubory LICENSE a
README. Soubor LICENSE říká, za jakých
podmínek můžou kouzelné věty použít ostatní čarodějové. Je hodně druhů
licencí a hodně rad, jak licenci
vybrat. Soubor README představuje repozitář:
Co je to a proč zrovna to, jak s tím pracovat
a komu psát dotazy.
Soubory se připraví ke sledování jejich historie příkazem
$ git add LICENSE READMEa aktuální stav repozitáře se zkontroluje příkazem
$ git status
On branch master
No commits yet
Changes to be committed:
(use "git rm --cached <file>..." to unstage)
new file: LICENSE
new file: README
Untracked files:
(use "git add <file>..." to include in what will be committed)
vetsi-nez.rktPříkaz git status ukáže tři skupiny souborů, ale každou
ze skupin vynechá, když do ní nespadá žádný soubor:
Z červeného uděláme zelený tak, že
$ git add JMENO-SOUBORUa naopak ze zeleného červený tak, že
$ git reset JMENO-SOUBORUZ příkazu git status je vidět, že soubory LICENSE a
README jsou připraveny k zaznamenání do historie repozitáře. Zaznamenáme
je příkazem:
$ git commit
[master (root-commit) 4535b31] Přidej licenci a readme
2 files changed, 30 insertions(+)
create mode 100644 LICENSE
create mode 100644 READMEkterý otevře textový editor, počká na krátkou zprávu a po uložení zprávy a ukončení textového editoru přidá soubory LICENSE a README do historie repozitáře.
Krátká zpráva má svá pravidla. První řádek je nadpis – začíná velkým písmenem, na konci není tečka, je maximálně 52 znaků dlouhý a je ve způsobu rozkazovacím. První řádek říká, co daná změna repozitáři provede. Krátká zpráva Přidej licenci a readme je celkem dobrá ukázka toho, jak může první řádek vypadat.
Pokud je potřeba rozvést co nebo proč se ukládá do historie repozitáře, za prvním řádkem následuje jeden prázdný řádek a pak odstavce, které to co a proč rozvedou. Ty už jsou zarovnané na 72 znaků.
Psát jak se změny provedou je zbytečné, protože čarodějové tráví dost času nad tím, aby kouzelné věty, které píší, byly hezké. A jak se to co provede, je přece zapsáno právě v kouzelných větách jednotlivých změn!
Stejným způsobem se přidá i soubor s řešením problému:
git add vetsi-nez.rkt
git commitHistorie repozitáře se prohlíží příkazem
$ git log
commit 591957744b7356c3169d86738c3b69f28d7e3dec (HEAD -> master, origin/master)
Author: Jméno Čaroděje <email@carodeje.xyz>
Date: Wed Jun 18 19:48:20 2025 +0200
Přidej řešení "Je větší 20 nebo číslo?"
commit 4535b310762c1cb4891e64af0b71368cd4cf8b4c
Author: Jméno Čaroděje <email@carodeje.xyz>
Date: Wed Jun 18 19:47:38 2025 +0200
Přidej licenci a readmeHistorie repozitáře sestává ze změn, kterým se říká commit.
Příkazem git show IDENTIFIKATOR-ULOZENE-ZMENY lze zobrazit
jednotlivé změny (commit). Konkrétně například:
$ git show 591957744b7356c3169d86738c3b69f28d7e3dec
commit 591957744b7356c3169d86738c3b69f28d7e3dec (HEAD -> master, origin/master)
Author: Jméno Čaroděje <email@carodeje.xyz>
Date: Wed Jun 18 19:48:20 2025 +0200
Přidej řešení "Je větší 20 nebo číslo?"
diff --git a/vetsi-nez.rkt b/vetsi-nez.rkt
new file mode 100644
index 0000000..9301738
--- /dev/null
+++ b/vetsi-nez.rkt
@@ -0,0 +1,9 @@
+#lang racket
+; Je větší 20 nebo číslo?
+(define dvacet 20)
+(define (větší-než číslo)
+ (if (> číslo dvacet)
+ (string-append "Větší je " (number->string číslo) ".")
+ (string-append "Větší je " (number->string dvacet) ".")))
+(větší-než 11)
+(větší-než 27)Pro základní nastavení:
$ git config --global user.name "Jméno Čaroděje"
$ git config --global user.email "email@carodeje.xyz".Vytvoření repozitáře:
$ git init
$ git statusSledování změn souborů:
$ git add JMENO-SOUBORU
$ git reset JMENO-SOUBORU
$ git commitHistorie rezpozitáře:
$ git log
$ git show IDENTIFIKATOR-ULOZENE-ZMENYČtení úzce souvisí se sebevzděláváním – čtení kouzelných vět ostatních čarodějů obohacuje čaroděje v chápání kouzelného jazyka i způsobů řešení problémů. Čtení historie repozitáře pak v tom, jak se repozitáře spravují a jak se kouzelné věty vylepšují.
Když nějaký čaroděj zabrousí do repozitáře jiného čaroděje nebo čarodějky, nejprve se zorientuje. Zkontroluje licenci a odhadne tak filosofii autora. Pak se podívá do souboru README, aby zjistil, o čem repozitář je a jak složité je jej použít. Prohlédnutím historie repozitáře čaroděj zjistí kdo, jak aktivně a jakým způsobem se na vývoji repozitáře podílí. A samozřejmě si čaroděj projde dopisy pro kouzelnou hůlku – zdrojové kódy. Když čaroděj něco hledá, většinou do zdrojových kódů koukne jako první.
Mezi čarodějnické konvence (dohody), které čarodějové dodržují, protože to zjednodušuje jejich spolupráci, patří i to, že když čaroděj vymýšlí nová kouzelná slova nebo když zaznamenává historii repozitáře, píše anglicky. To proto, že hodně kouzelných slov kouzelných jazyků je převzato z angličtiny. Navíc si díky této konvenci rozumí čarodějové a čarodějky celého světa.
Čarodějové a čarodějky svoje repozitáře sdílí přes webové stránky, jako je třeba https://codeberg.org/Neprogramator/vetsi-nez/. Pokud ostatní čarodějové webovou stránku znají, mohou si repozitář zkopírovat programem Git:
$ git clone https://codeberg.org/Neprogramator/vetsi-nez
Cloning into 'vetsi-nez'...
remote: Enumerating objects: 7, done.
remote: Counting objects: 100% (7/7), done.
remote: Compressing objects: 100% (7/7), done.
remote: Total 7 (delta 1), reused 0 (delta 0), pack-reused 0 (from 0)
Receiving objects: 100% (7/7), done.
Resolving deltas: 100% (1/1), done.
Z kouzelného dopisu, který čaroděj kouzelné hůlce napsal, může kouzelná hůlka vytvořit kouzelný lektvar – spustitelný soubor. Dokumentace kouzelného jazyka Racket popisuje, jak na to. A samozřejmě jde lektvary vytvořit i ve vývojovém prostředí DrRacket.
Čarodějové se při psaní dopisů mohou splést. Vlastně se pletou dost často. Otázka tak není, jestli kouzelný dopis obsahuje chyby, protože odpověď je ano. Ta správná, důležitá otázka zní – jak snadno se chyby najdou a hlavně – jak rychle se dají opravit? S hledáním a opravováním chyb pomáhá testování. Dokumentace kouzelného jazyka Racket popisuje, jak takové testování zařídit.
Problém, pro jehož řešení napsaném v kouzelném jazyce Racket vytvoří kouzelná hůlka kouzelný lektvar, tedy spustitelný soubor, může být:
Podstatné jméno (číslo) 20 je pojmenované jako
dvaceta nové kouzelné slovesovětší-nežpracuje s jedním podstatným jménem (parametrem)číslo: jestli ječíslovětší neždvacet, kouzelné slovesovětší-nežvrátí nové podstatné jméno (text)"Větší je číslo.", kdečíslov textu je nahrazené konkrétní aktuální hodnotou; jinak vrátí"Větší je 20.".
Řešením takového problému, zapsaném v kouzelném jazyce Racket v dopisu pro kouzelnou hůlku, může být třeba:
#lang racket
; Je větší 20 nebo číslo?
(define dvacet 20)
(define (větší-než číslo)
(if (> číslo dvacet)
(string-append "Větší je " (number->string číslo) ".")
(string-append "Větší je " (number->string dvacet) ".")))
(větší-než 11)
(větší-než 27)Protože dopis pro kouzelnou hůlku píšeme v DrRacket, je potřeba, aby
první řádek byl #lang racket.
Kouzelnou hůlku poprosíme o vykonání kouzelného dopisu klávesovou
zkratkou Ctrl + R nebo z menu Racket -> Run.
Výsledek je potom:
"Větší je 20."
"Větší je 27."A z minulé kapitoly lze proto s výhodou použít postup řešení:
$ git log
commit 591957744b7356c3169d86738c3b69f28d7e3dec (HEAD -> master, origin/master)
Author: Jméno Čaroděje <email@carodeje.xyz>
Date: Wed Jun 18 19:48:20 2025 +0200
Přidej řešení "Je větší 20 nebo číslo?"
commit 4535b310762c1cb4891e64af0b71368cd4cf8b4c
Author: Jméno Čaroděje <email@carodeje.xyz>
Date: Wed Jun 18 19:47:38 2025 +0200
Přidej licenci a readmeSamozřejmě při splnění podmínek licence.
Spustitelný soubor se v DrRacket vytvoří kliknutím v menu Racket -> Create Executable…. Tím se otevře okno, kde stačí ponechat výchozí hodnoty a kliknout na Create.
V repozitáři vetsi-nez se pak objeví nový soubor
vetsi-nez, který spustíme z příkazové řádky:
$ ./vetsi-nez
"Větší je 20."
"Větší je 27."Když čaroděj do dopisu pro kouzelnou hůlku přidává testy, nejprve na to kouzelnou hůlku upozorní. To udělá tak, že na začátek dopisu přidá kouzelnou větu:
(module+ test (require rackunit))Když chce potom čaroděj otestovat, že výsledek vykonání kouzelné věty
odpovídá tomu, co očekává, použije kouzelné sloveso check-equal?:
(module+ test
(check-equal? (větší-než 11)
"Větší je 20."))Přidání testů výsledek vykonání kouzelného dopisu nezmění:
"Větší je 20."
"Větší je 27."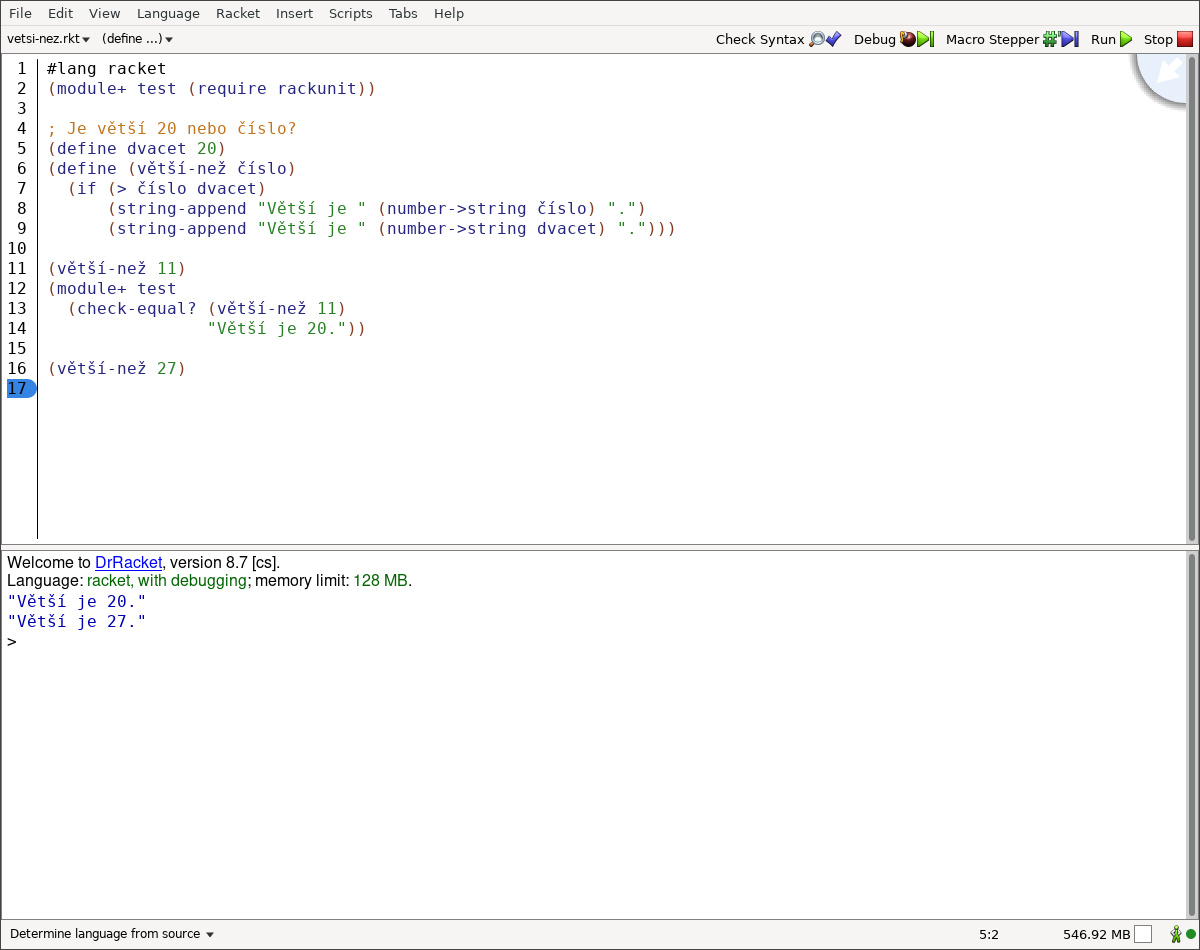
Jak tedy čaroděj pozná, když udělá chybu? Když otestuje kouzelnou větu, která neplatí…
(module+ test
(check-equal? (větší-než 27)
"Větší je 20."))… kouzelná hůlka jej upozorní:
"Větší je 20."
"Větší je 27."
--------------------
. FAILURE
name: check-equal?
location: vetsi-nez.rkt:15:2
actual: "Větší je 27."
expected: "Větší je 20."
--------------------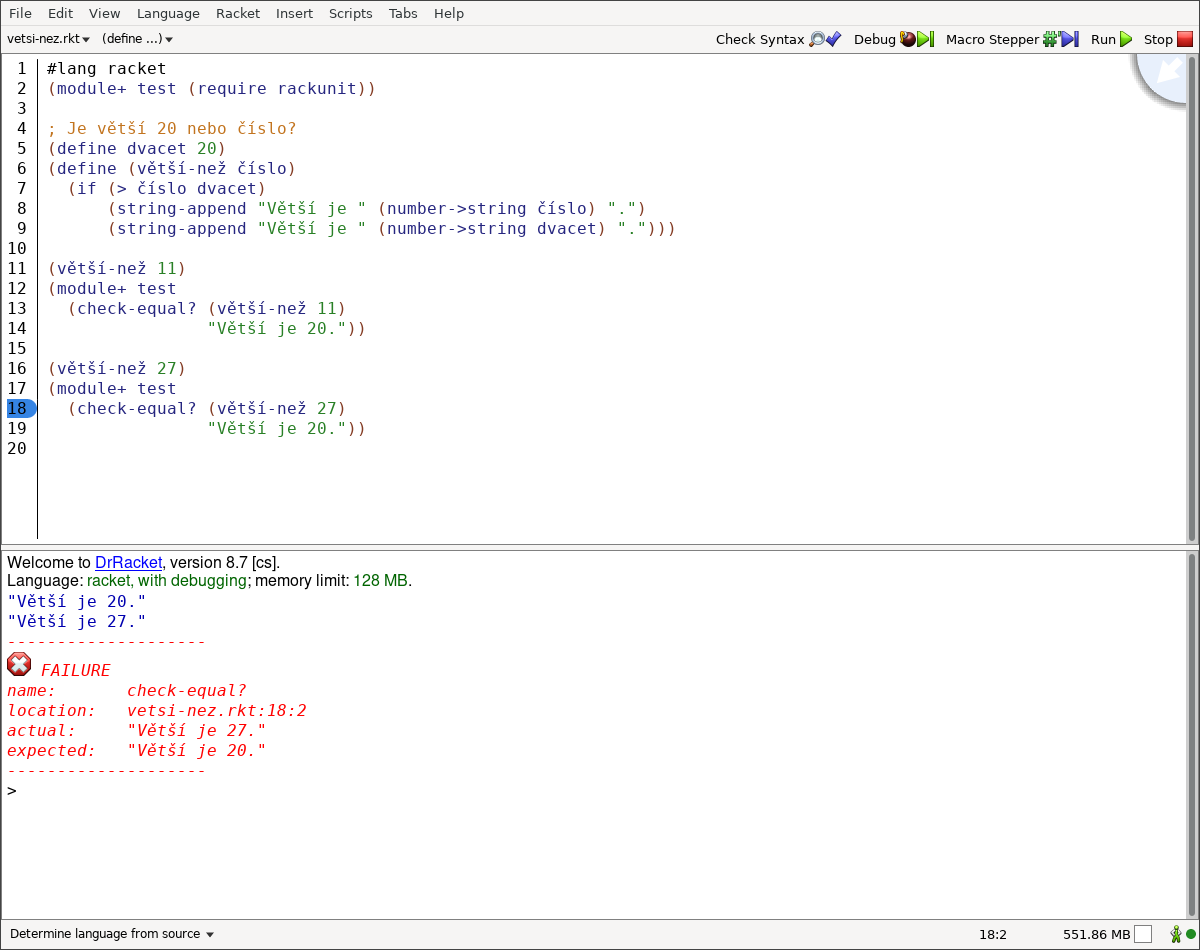
Vlastně je od kouzelné hůlky hezké, že čaroděje obtěžuje jen tehdy, když je to nezbytně nutné.
Repozitář s testy lze prozkoumat na https://codeberg.org/Neprogramator/vetsi-nez-s-testy/ nebo pomocí Git:
git clone https://codeberg.org/Neprogramator/vetsi-nez-s-testy.gitTeď už bychom měli znát všechny čtyři oblasti čarodějnického řemesla: psaní zdrojového kódu a dokumentace, zaznamenávání historie změn, vytváření spustitelných souborů a psaní testů.
Zdrojový kód se jednou napíše a pak mnohokrát čte, vylepšuje a opravuje, protože programy je třeba udržovat. Technologie zastarávají a čarodějové stárnou, takže pokud má program technologie a čaroděje přežít, je potřeba, aby zdrojový kód programu pochopili další a další čarodějové.
Spolupráce čarodějů je nesmírně důležitá, pokud má jejich program změnit svět; žádný čaroděj nenapíše program, který změní svět, sám. Základ spolupráce čarodějů je sdílení změn v kouzelných větách, tedy sdílení změn částí zdrojového kódu. To úzce souvisí se zaznamenáváním historie, protože to, co mezi sebou čarodějové ve skutečnosti sdílí, je historie změn, o které jsou přesvědčení, že vylepší zdrojový kód. No a spolupráce spočívá v tom, že se zeptají ostatních čarodějů, jestli si to myslí také.
Aby byli čarodějové užiteční, je potřeba, aby pomáhali ostatním. To dělají tím, že z kouzelných vět, zdrojových kódů, vytváří lektvary, programy, které může spustit každý.
Nakonec – čarodějové dělají chyby. A dělají je dost často. Aby chyby rychle našli, vymysleli testy. Testy jsou (zase jen) kouzelné věty, které utvrdí čaroděje v tom, že kouzelné věty, které vymyslel, dělají to, co dělat mají.
Kouzelná hůlka je až neuvěřitelně rychlá a přesná. I kdyby se čaroděj
snažil sebevíc, kouzelnou větu (+ 123 456)
vyhodnotí kouzelná hůlka rychleji a bez chyb. A co teprve (* 123 456)!
Navíc se čarodějové snaží psát kouzelné věty chytře – aby jich napsali málo, ale kouzelná hůlka aby toho udělala hodně. Takže učí kouzelnou hůlku, aby kouzelné věty vykonávala pořád dokola, nebo aby zpracovala velké množství informací najednou.
Čarodějové často potřebují vykonat nějakou kouzelnou větu znovu a znovu a znovu. Psát stejné kouzelné věty pod sebe je nudné a navíc není vždy jasné, kolik kouzelných vět bude nakonec potřeba. V takových situacích čarodějové naučí kouzelnou hůlku nové kouzelné sloveso, které použijí na to, aby kouzelnou hůlku ono nové kouzelné sloveso naučili.
Kouzelná podstatná jména ukrývají informace, které chce čaroděj získat. Většinou chce čaroděj získat více než jednu informaci, a tak potřebuje kouzelná podstatná jména spojit. Před první kouzelné podstatné jméno přidá druhé, před druhé přidá třetí, před třetí přidá čtvrté a tak dále a tak dále a tak dále…
Čarodějové si velmi rádi usnadňují práci. Třeba taková chůze do schodů je únavná, a tak typického čaroděje nenapadne nic lepšího, než říci kouzelné hůlce, aby to udělala za něj.
Čarodějové dost často bydlí v různých poschodích a potřebují tedy vystoupat různý počet schodů. Navíc ale rádi sdílejí své umění s ostatními. Tohle dilema nakonec vyřešil jeden čaroděj tím, že vymyslel kouzelnou větu
(define (vyjdi-schod ze-schodu)
(+ 1 ze-schodu))kterou kouzelné hůlce předal několikrát za sebou, protože aby se dostal domů, musí vyjít tři schody:
(vyjdi-schod 0) (vyjdi-schod 1) (vyjdi-schod 2)Výsledek, který je v DrRacket vidět v REPL, je:
1
2
3Kouzelná věta která začíná kouzelným slovesem vyjdi-schod se tak hodí i čarodějovi,
který potřebuje vystoupat pět schodů. Jednoduše kouzelné hůlce předá
kouzelnou větu vícekrát:
(vyjdi-schod 0)
(vyjdi-schod 1)
(vyjdi-schod 2)
(vyjdi-schod 3)
(vyjdi-schod 4)s výsledkem:
1
2
3
4
5Když kouzelná hůlka vykoná kouzelnou větu začínající slovesem vyjdi-schod, výsledek je číslo schodu,
na kterém se čaroděj ocitne. Když jde čaroděj domů, vždycky začíná v
přízemí.
(define přízemí 0)Když má čaroděj k dispozici kouzelné sloveso vyjdi-schod a kouzelné podstatné jméno
přízemí, může nechat kouzelnou
hůlku, aby jej dostala do třetího poschodí kouzelnými větami
(vyjdi-schod přízemí)
(vyjdi-schod 1)
(vyjdi-schod 2)Pomocí kouzelného slovesa let* z kapitoly
Pojmenování informací: definice proměnných může
čaroděj místo 1 a 2 použít
kouzelná podstatná jména první-schod a druhý-schod:
(let* ((první-schod (vyjdi-schod přízemí))
(druhý-schod (vyjdi-schod první-schod)))
(vyjdi-schod druhý-schod))Výsledek je potom: 3
A protože výsledek vykonání kouzelné věty je nějaké slovo kouzelného jazyka, může čaroděj výsledné slovo použít v další kouzelné větě a vytvořit tak jednu dlouhou mocnou kouzelnou větu:
(vyjdi-schod (vyjdi-schod (vyjdi-schod přízemí)))Výsledek je stejný, tedy: 3
Tenhle přístup ale rozhodně netěší úplně všechny čaroděje. A obzvláště netěší ty, co bydlí v mrakodrapu, a musí proto domů vystoupat 20 schodů:
(vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod
(vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod
(vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod
(vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod
přízemí))))))))))))))))))))Teď je nejspíš ten nejlepší čas na kouzelnický trik. Zkušenější čarodějové si dovedou představit, co asi tak kouzelná hůlka provede s kouzelnou větou, kterou čaroděj napíše nebo si někde přečte. A nebo taky ne.
Když jsou čarodějové v koncích a kouzelná hůlka po vykonání kouzelné věty odpovídá úplně něco jiného, než čaroděj očekává, může čaroději v pochopení kouzelné věty pomoci vývojové prostředí (v našem případě DrRacket) a jeho debugger. Debugger čaroději pomůže projít dopis pro kouzelnou hůlku krok za krokem.
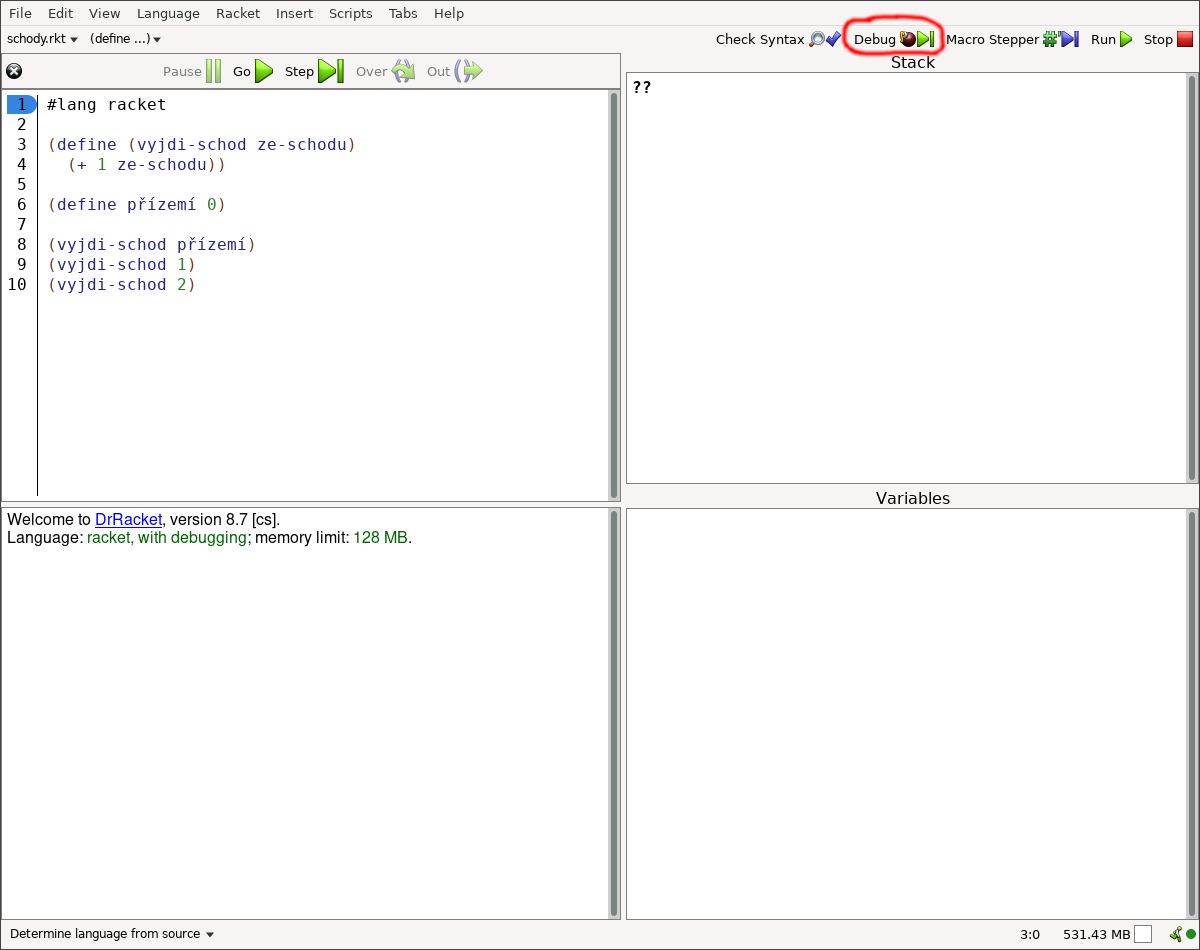
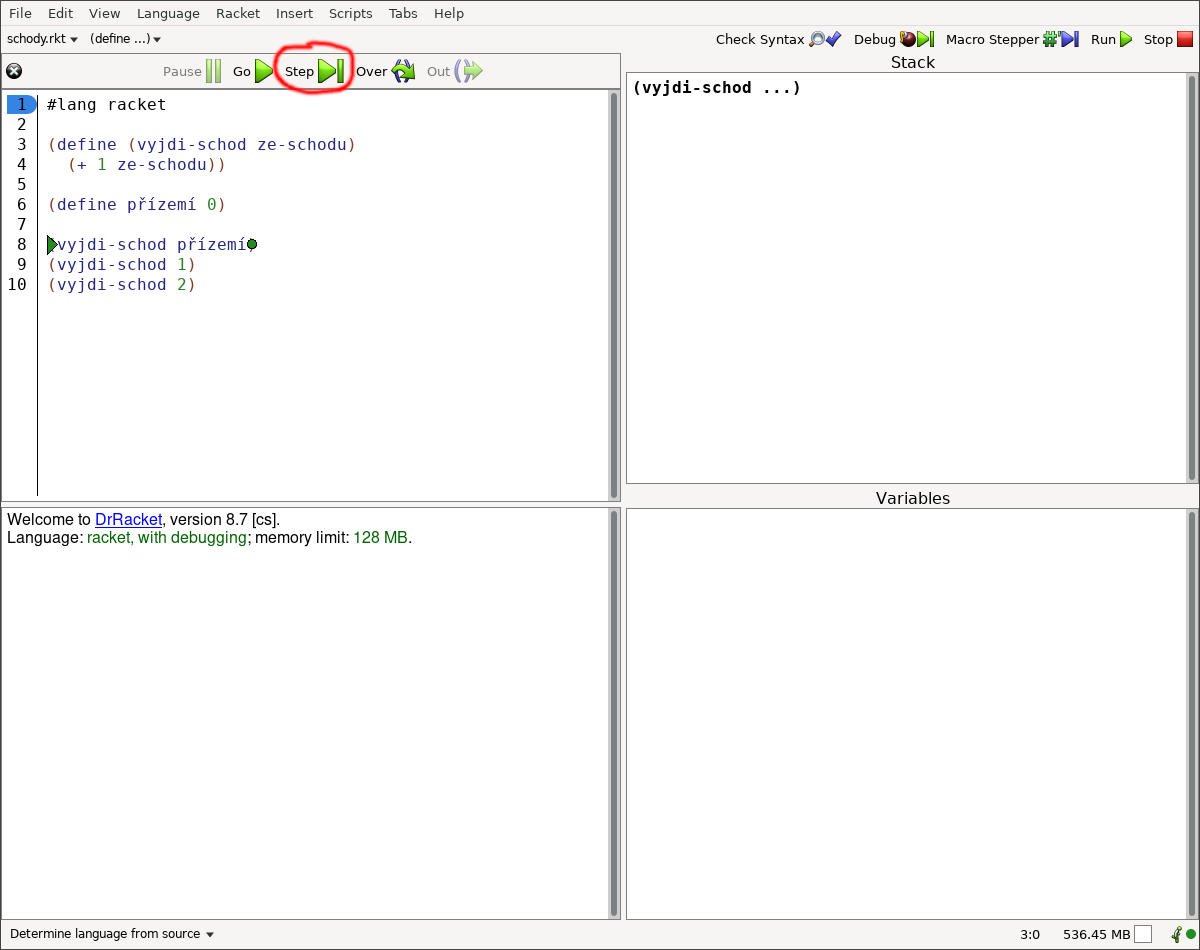
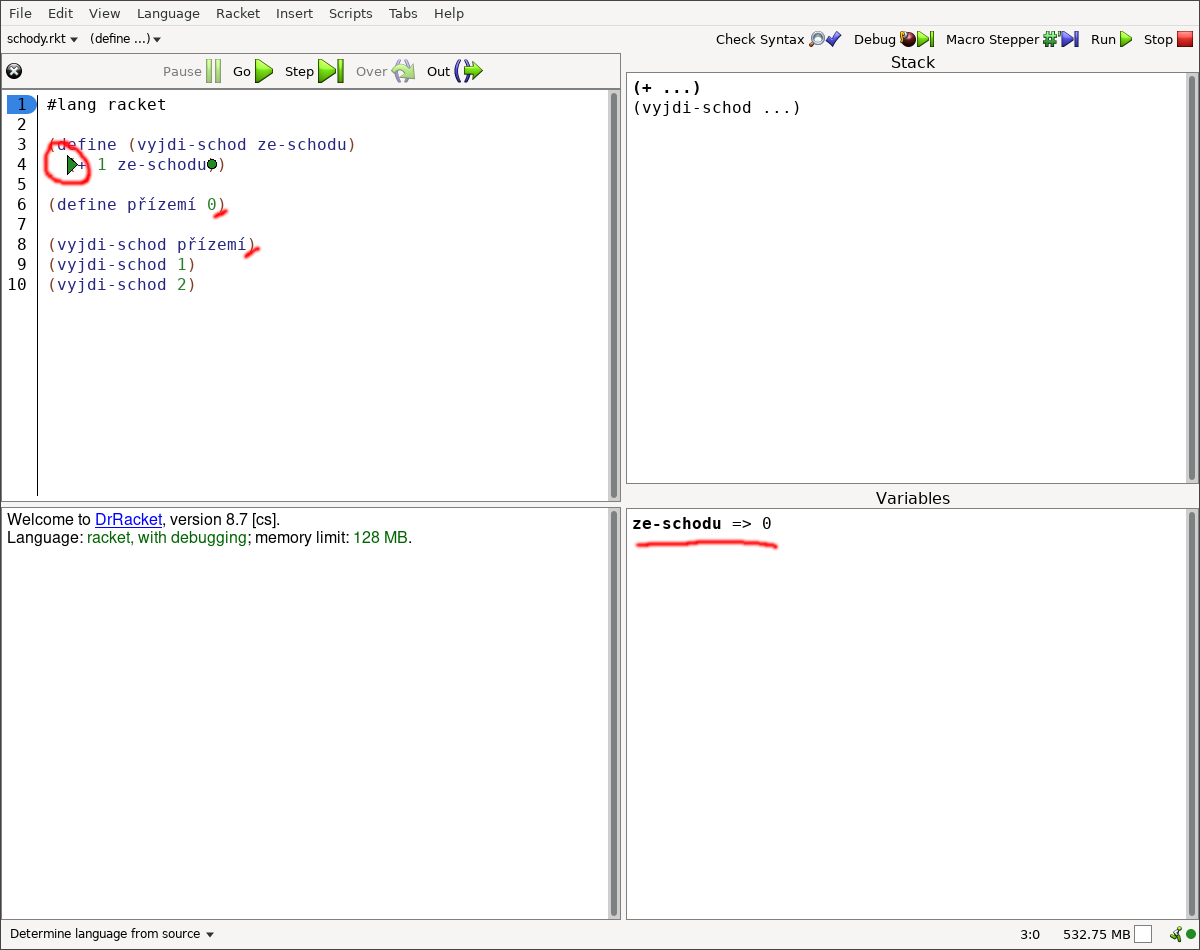
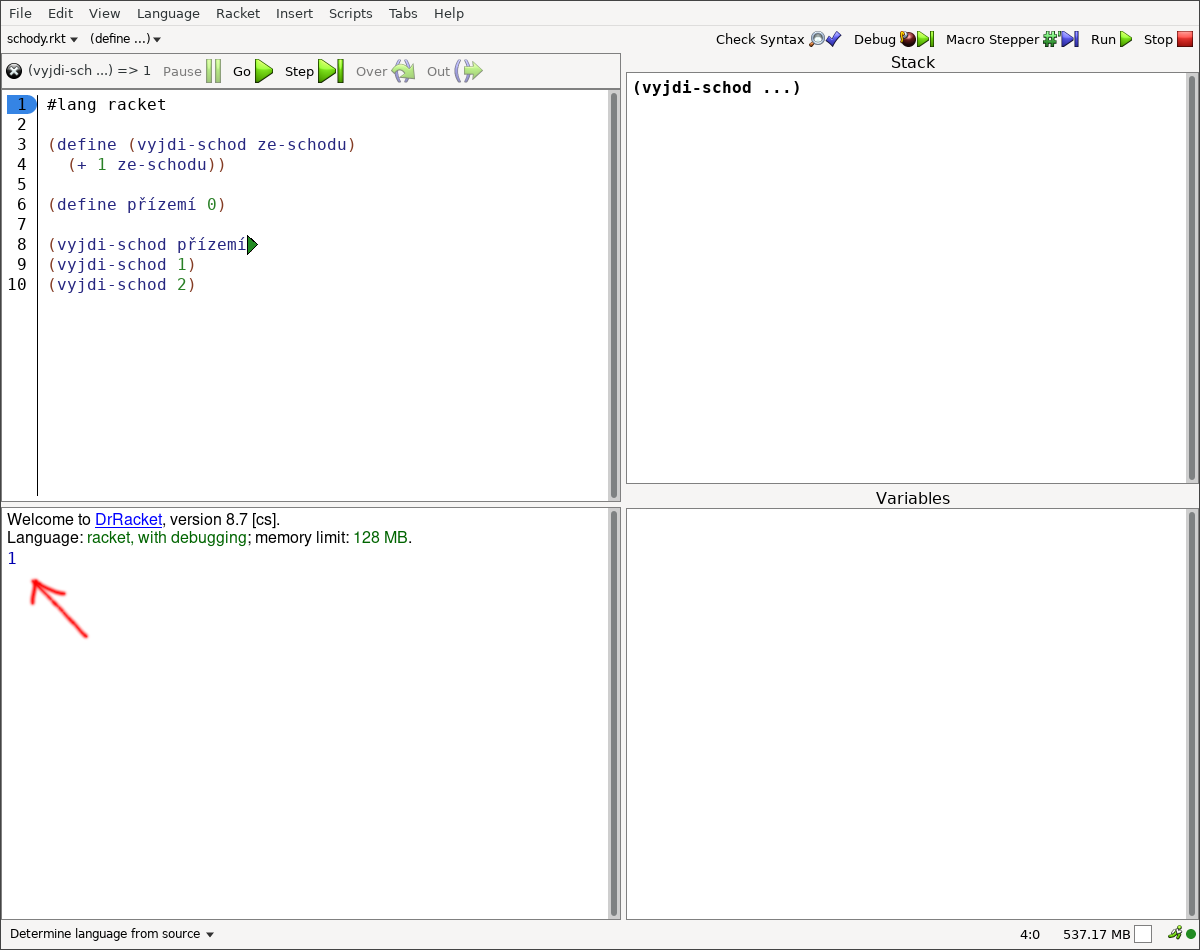
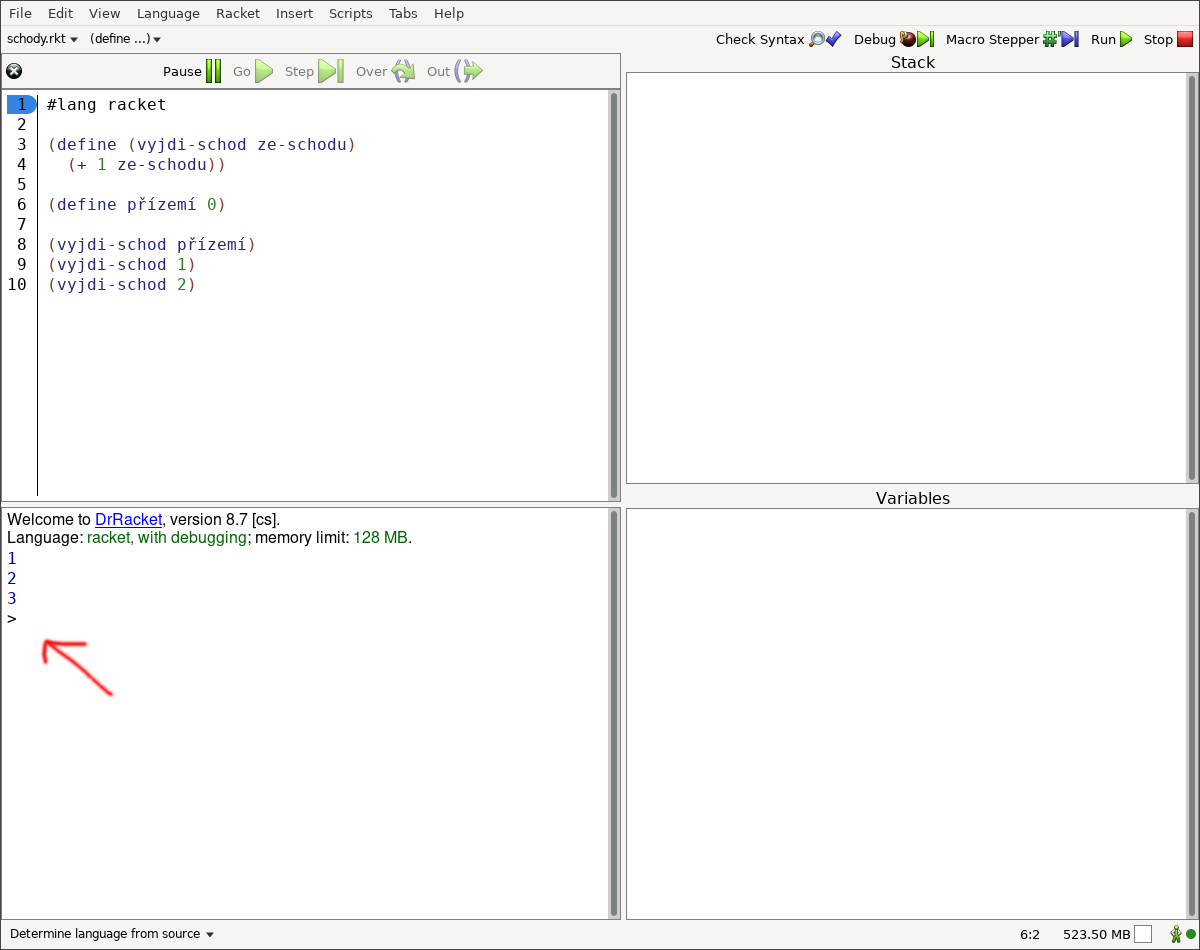
Obrázky (občas se říká screenshoty) vývojového prostředí DrRacket z krokování (občas se říká ladění nebo debugování) dopisu pro kouzelnou hůlku (občas se říká zdrojového kódu) zabíraly spoustu místa. Nerad dávám domácí úkoly, ale neprogramátor by si teď měl krok za krokem projít:
#lang racket
(define (vyjdi-schod ze-schodu)
(+ 1 ze-schodu))
(define přízemí 0)
(let* ((první-schod (vyjdi-schod přízemí))
(druhý-schod (vyjdi-schod první-schod)))
(vyjdi-schod druhý-schod))a určitě také:
#lang racket
(define (vyjdi-schod ze-schodu)
(+ 1 ze-schodu))
(define přízemí 0)
(vyjdi-schod (vyjdi-schod (vyjdi-schod přízemí)))Krátká technická poznámka: První řádek dopisu pro kouzelnou hůlku,
tedy #lang racket, je typický pro
programovací jazyk Racket. Programovací jazyk Racket
rozšiřuje jiný programovací jazyk, Scheme, který #lang ...
nepoužívá.
Je zajímavé si při tom všimnou okna Stack (vpravo nahoře). Okno Stack říká, v jaké kouzelné větě se právě nachází kouzelná hůlka, která kouzelné věty vykonává. (V okně se zdrojovým kódem je aktuálně vykonávaná věta označena zeleným trojúhelníkem na začátku a zeleným kolečkem na konci. V okně Stack je vyznačena tučně.)
Třeba
(vyjdi-schod ...)
(let* ...)říká, že kouzelná hůlka ve větě začínající kouzelným slovesem let* narazila
na kouzelnou větu začínající kouzelným slovesem vyjdi-schod a nejprve musí vykonat
kouzelnou větu začínající vyjdi-schod, aby mohla pokračovat ve
vykonávání kouzelné věty začínající kouzelným slovesem let*.
Podobně je to i v případě, když okno Stack zobrazí
(+ ...)
(vyjdi-schod ...)
(let* ...)protože kouzelná věta, která začíná kouzelným slovesem vyjdi-schod, a zároveň je v tomto
případě uvnitř kouzelné věty začínající let*, obsahuje
kouzelnou větu, která začíná kouzelným slovesem +.
Když čaroděj krokuje mocnou kouzelnou větu
(vyjdi-schod (vyjdi-schod (vyjdi-schod přízemí)))zobrazí se v okně Stack dokonce čtyři řádky:
(+ ...)
(vyjdi-schod ...)
(vyjdi-schod ...)
(vyjdi-schod ...)Jedním ze způsobů, jakým čaroděj vytvoří dlouhou mocnou kouzelnou větu je, že čaroděj do kouzelné věty vnoří další kouzelnou větu. Vnořená kouzelná věta jistě může začínat stejným kouzelným slovesem, jako třeba:
(vyjdi-schod (vyjdi-schod (vyjdi-schod přízemí)))Čaroděj bydlící až na dvacátém schodu, musí vět vnořit více:
(vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod
(vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod
(vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod
(vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod (vyjdi-schod
přízemí))))))))))))))))))))Když ale čaroděj, nebo i ne-čaroděj, stoupá po schodech domů, tak
schody nepočítá. Že je doma, pozná ne-čaroděj podle vstupních dveří.
Nebo rohožky. No a čaroděj se zeptá kouzelné hůlky, třeba kouzelnou
větou začínající kouzelným slovesem jsem-doma?, na kterou odpoví kouzelná
hůlka: #t
nebo #f
Pro čaroděje bydlícím na třetím schodu tak ke kouzelnému slovesu
vyjdi-schod přibude:
(define (jsem-doma? schod)
(= 3 schod))a pro čaroděje bydlícím na dvacátém schodu:
(define (jsem-doma? schod)
(= 20 schod))No a když čaroděj naučil kouzelnou hůlku kouzelným slovesům vyjdi-schod a jsem-doma?, chtěl by, aby kouzelná
hůlka pochopila, když ji čaroděj řekne (stoupej-dokud-nejsem-doma přízemí).
Chtěl by, aby na takovou větu kouzelná hůlka odpověděla: 3
Nebo: 20
A tak kouzelnou hůlku naučí:
(define (stoupej-dokud-nejsem-doma ze-schodu)
(if (jsem-doma? ze-schodu)
ze-schodu ; jsem doma!
(stoupej-dokud-nejsem-doma (vyjdi-schod ze-schodu))))Krátká technická poznámka: Středník ; značí
komentář. Vše za ním, až do konce řádky, kouzelná hůlka
ignoruje. Čarodějové tak sdílí poznámky, které jsou určené ostatním
čarodějům a kouzelná hůlka o nich nemá vědět.
Celý dopis pro kouzelnou hůlku, který píše čaroděj bydlící ve třetím patře, tedy zní:
#lang racket
(define (vyjdi-schod ze-schodu)
(+ 1 ze-schodu))
(define přízemí 0)
(define (jsem-doma? schod)
(= 3 schod))
(define (stoupej-dokud-nejsem-doma ze-schodu)
(if (jsem-doma? ze-schodu)
ze-schodu ; jsem doma!
(stoupej-dokud-nejsem-doma (vyjdi-schod ze-schodu))))Když potom čaroděj kouzelné hůlce napíše
(stoupej-dokud-nejsem-doma přízemí)kouzelná hůlka odpoví: 3
Čaroděj bydlící ve dvacátém patře napíše ten samý dopis, jen trochu
změní jsem-doma?, protože bydlí
výše.
V tuhle chvíli je dobrý nápad v DrRacket spustit debugger. Určitě
není potřeba všechno hned pochopit. Jistě se ale vyplatí se teď trochu
potrápit a sledovat, jaká kouzelná věta se při kterém kroku vykonává
(zelený trojúhelník a kolečko a tučný řádek v okně Stack),
jakou hodnotu právě mají kouzelná podstatná jména (proměnné, okno
Variables) a jak to všechno dopadne (okno s výsledkem, kde je
nakonec >).
Čaroděj tedy kouzelnou hůlku naučil stoupej-dokud-nejsem-doma. Aby
kouzelnou hůlku nové kouzelné sloveso naučil, použil čaroděj kouzelná
slovesa jsem-doma?, vyjdi-schod a … stoupej-dokud-nejsem-doma! Takovému
přístupu se říká rekurze.
Rekurze je mocná a nebezpečná. Mocná proto, že pomáhá čarodějům
bydlícím ve dvacátém patře se psaním dopisů pro kouzelnou hůlku.
Nebezpečná proto, že se může stát, že čaroděj bude stále stoupat vzhůru
a nikdy se domů nedostane. Třeba když bydlí ve sklepě a číslo schodu je
tak -1.
Proč se čaroděj bydlící ve sklepě nikdy nedostane domů? Protože
čaroděj v kouzelném dopise říká kouzelné hůlce (stoupej-dokud-nejsem-doma přízemí).
Kouzelné podstatné jméno přízemí
je 0 a
kouzelné sloveso vyjdi-schod
způsobí, že čaroděj vystoupá o schod výše. Čaroděj proto nikdy neklesá a
z přízemí 0 se tak nemůže
dostat do sklepa -1.
To, aby kouzelná hůlka vykonávání rekurzivní kouzelné věty dokončila,
zajišťuje ukončující podmínka. V případě kouzelné věty
začínající kouzelným slovesem stoupej-dokud-nejsem-doma je ukončující
podmínka jsem-doma?. V každém
kroku kouzelná hůlka zkontroluje, jestli se čaroděj ze-schodu dostane domů. Pokud ano,
odpoví kouzelná hůlka ze-schodu,
tedy číslo schodu, na kterém čaroděj právě stojí. Jestliže ale kouzelná
hůlka vykoná kouzelnou větu (jsem-doma? ze-schodu) a ona kouzelná
věta neplatí – výsledek vykonání kouzelné věty je #f – kouzelná
hůlka provede rekurzivní krok: znovu vykoná kouzelnou větu
začínající kouzelným slovesem stoupej-dokud-nejsem-doma, tentokrát
ale ze schodu (vyjdi-schod ze-schodu), tedy ze schodu
o jeden výše.
V tuhle chvíli je dobrý nápad znovu v DrRacket spustit debugger.
Navíc je asi také ten správný čas zmínit Indukci,
protože rekurze je paralela matematické indukce. První krok
matematické indukce odpovídá tomu, když platí ukončující podmínka.
Indukční krok pak zajišťuje pokračování ve vykonávání
rekurzivní funkce v případě, že ukončující podmínka neplatí.
Indukčnímu kroku se říká rekurzivní krok nebo rekurzivní
volání funkce. Rekurzivní funkce je v tomto případě stoupej-dokud-nejsem-doma.
Rekurze je, když čaroděj používá nové kouzelné sloveso ve chvíli, kdy kouzelnou hůlku ono nové kouzelné sloveso učí:
(define (počítej-do-dvaceti z-čísla)
(if (= 20 z-čísla)
z-čísla
(počítej-do-dvaceti (+ 1 z-čísla))))Na kouzelnou větu
(počítej-do-dvaceti 11)pak kouzelná hůlka odpoví: 20
Rekurzivní funkce je počítej-do-dvaceti a ukončující
podmínka je (= 20 z-čísla).
Kouzelná věta (počítej-do-dvaceti (+ 1 z-čísla))
je rekurzivní krok.
Rekurze se dá použít kdekoli je potřeba nějaké opakování a typickým příkladem může být kouzelná věta
(sečti-čísla-mezi 3 6)na kterou má kouzelná hůlka odpovědět: 18
Kouzelné sloveso sečti-čísla-mezi naučí čaroděj
kouzelnou hůlku kouzelnou větou:
(define (sečti-čísla-mezi menší větší) ; včetně
(if (= menší větší)
větší
(+ menší (sečti-čísla-mezi (+ 1 menší) větší))))Rekurzivní funkce sečti-čísla-mezi má ukončující
podmínku (= menší větší)
a rekurzivní krok je kouzelná věta:
(+ menší (sečti-čísla-mezi (+ 1 menší) větší))Seznam je několik kouzelných slov dohromady. Čarodějové
vytváří seznamy pomocí kouzelných vět začínajících kouzelným slovesem
list.
Jako třeba čarodějův nákupní seznam:
(list "sýr" "rýže" "zelí" "čaj")Výsledkem vykonání takové kouzelné věty je kouzelné podstatné jméno
'("sýr" "rýže" "zelí" "čaj")které začíná apostrofem '
a pak vypadá jako kouzelná věta se špatnou gramatikou, protože jí chybí
sloveso.
Seznam je tedy kouzelné podstatné jméno, které začíná
apostrofem a závorkou '(,
pokračuje výčtem kouzelných slov oddělených mezerami a končí zase
závorkou ).
Seznam seskládá z kouzelného slova, které je v seznamu první, a z dalšího seznamu, který je tvořen zbylými kouzelnými slovy.
První kouzelné slovo ze seznamu získáme pomocí car. Kouzelná
hůlka na kouzelnou větu
(car (list "sýr" "rýže" "zelí" "čaj"))odpoví: "sýr"
Pro získání zbytku kouzelných slov slouží cdr, takže
na
(cdr (list "sýr" "rýže" "zelí" "čaj"))odpoví kouzelná hůlka: '("rýže" "zelí" "čaj")
Seznam je kouzelné podstatné jméno, takže je v pořádku, že je v
kouzelné větě až po kouzelném slovesu car nebo cdr. Položky
seznamu jsou ale kouzelná slova – mohou to být kouzelná podstatná jména,
jako v nákupním seznamu čaroděje, ale i kouzelná slovesa.
Seznam, který nemá žádnou položku, je prázdný seznam. Vytvoří se
kouzelnou větou začínající kouzelným slovesem list, která ale
nemá žádná další kouzelná slova:
(list)Kouzelná hůlka pak odpoví: '()
Zda je seznam prázdný zjistí čaroděj kouzelnou větou začínající
kouzelným slovesem null?. Na
kouzelnou větu
(null? (list))odpoví kouzelná hůlka: #t
Nakonec to chce prozkoumat car a cdr v
souvislosti se seznamy různých délek.
Na (car '("zelí" "čaj"))
odpoví kouzelná hůlka: "zelí"
Na (cdr '("zelí" "čaj"))
řekne: '("čaj")
protože i když zbytek seznamu obsahuje jenom jednu položku, je to pořád
seznam.
Výsledek vykonání (car '("čaj"))
je: "čaj"
A z kouzelné věty (cdr '("čaj"))
udělá kouzelná hůlka: '()
Co s kouzelnou větou (car '())?
Kouzelná hůlka řekne:
car: contract violation
expected: pair?
given: '()Tedy: “Chyba! Prázdný seznam nemá první položku!”
Stejně tak má kouzelná hůlka výhrady vůči kouzelné větě (cdr '()),
na kterou odpoví:
cdr: contract violation
expected: pair?
given: '()Což je: “Chyba! Prázdný seznam nemá zbytek!”
Čarodějové používají seznamy velmi často – líbí se jim více kouzelných slov v jednom podstatném jméně. Klasický kouzelnický učebnicový příklad práce se seznamem je zjištění délky seznamu:
(délka-seznamu (list "sýr" "rýže" "zelí" "čaj"))Jenže kouzelná hůlka takové kouzelné sloveso nezná a odpoví:
délka-seznamu: undefined;Velkou částí práce čaroděje je hledat, co se v problémech, které
řeší, opakuje. Zkušenější čaroděj v problému délky seznamu opakování
pozná hned: nejkratší možný seznam, prázdný seznam (list), má
délku 0;
vždy po přidání nějaké položky do seznamu se délka takového seznamu
zvětší o 1.
Čaroděje takové rekurzivní přemýšlení přivede k
nápadu, jak kouzelnou hůlku kouzelné sloveso délka-seznamu naučit: Když je seznam
prázdný, jeho délka je 0. Pokud
prázdný není, jeho délka je délka zbytku seznamu + 1:
(define (délka-seznamu seznam)
(if (null? seznam)
0
(+ 1 (délka-seznamu (cdr seznam)))))Když to pak čaroděj zkusí znovu a na délku nákupního seznamu se kouzelné hůlky zeptá stejnou kouzelnou větou
(délka-seznamu (list "sýr" "rýže" "zelí" "čaj"))kouzelná hůlka už bude vědět a odpoví: 4
Délka seznamu je klasický kouzelnický učebnicový příklad práce se
seznamem proto, že kouzelná hůlka kouzelné sloveso pro zjištění délky
seznamu zná – je to length a
čarodějové jej používají dost často. Proto na kouzelnou větu
(= (délka-seznamu (list "sýr" "rýže" "zelí" "čaj"))
(length (list "sýr" "rýže" "zelí" "čaj")))odpoví kouzelná hůlka: #t
Zjistit délku seznamu znamemá spočítat počet jeho položek. Prázdný
seznam má 0 položek; pro
každou položku seznamu se jeho délka zvětší o + 1.
Říká se, že kouzelná hůlka projde seznam a každou položku
seznamu použije. Pro délku seznamu použít znamená
přičíst + 1.
V kouzelnickém obchodě zaplatí čaroděj za každou položku tolik, kolik
má položka písmen. Proto čaroděje dost zajímá, kolik písmen dohromady
jeho nákupní seznam má. Pro každou položku seznamu tak místo + 1
použije čaroděj string-length:
(define (kolik-písmen-seznamu seznam)
(if (null? seznam)
0
(+ (string-length (car seznam))
(kolik-písmen-seznamu (cdr seznam)))))Na kouzelnou větu
(kolik-písmen-seznamu (list "sýr" "rýže" "zelí" "čaj"))pak kouzelná hůlka odpoví: 14
Nakonec by čaroděje mohlo ještě zajímat kolik jej stojí jednotlivé
položky. A my bychom mohli projít nákupní seznam, z každé položky pomocí
string-length
zjistit cenu položky a všechny ceny postupně spojit do nového seznamu
čísel. To by šlo.
Nejdřív je potřeba rekurzivně promyslet, jak kouzelné sloveso seznam->čísla kouzelnou hůlku
naučit. Kdy procházení skončí? Když je nákupní-seznam prázdný. Když je nákupní-seznam prázdný, co je výsledek
výkonání (seznam->čísla (list))?
Nový prázdný seznam (list).
To byla ukončující podmínka. Teď rekurzivní krok.
Cenu položky z nákupního seznamu zjistíme kouzelným slovesem string-length.
Zbytek nového seznamu, tedy zbývající ceny zbylých položek nákupního
seznamu, zjistíme rekurzivně kouzelným slovesem seznam->čísla, které se právě
snažíme naučit kouzelnou hůlku. Novou cenu položky a zbytek nového
seznamu spojíme do nového seznamu kouzelným slovesem cons.
(define (seznam->čísla nákupní-seznam)
(if (null? nákupní-seznam)
(list)
(cons (string-length (car nákupní-seznam))
(seznam->čísla (cdr nákupní-seznam)))))Kouzelná hůlka teď čarodějovi ráda poskytne informaci o cenách jednotlivých položek nákupního seznamu a na kouzelnou větu
(seznam->čísla (list "sýr" "rýže" "zelí" "čaj"))odpoví: '(3 4 4 3)
Pro ověření, že nám vše funguje, jak má, poslouží kouzelná věta
(= (kolik-písmen-seznamu (list "sýr" "rýže" "zelí" "čaj"))
(sečti-čísla-seznamu
(seznam->čísla (list "sýr" "rýže" "zelí" "čaj"))))na kterou má kouzelná hůlka odpovědět: #t
Je ale potřeba kouzelnou hůlku naučit sečti-čísla-seznamu:
Omlouváme se, tady je jediné místo v knize,
kde nám došel inkoust.
Seznam je kouzelné podstatné jméno, které obsahuje další kouzelná slova.
Vypadá trochu jako kouzelná věta, ale nemá sloveso a začíná
apostrofem a závorkou '(, za
kterými následují kouzelná slova oddělená mezerami a nakonec zase
závorka ).
Čarodějové rádi používají seznamy spolu s rekurzí, protože jim pomáhají vyjádřit problémy, které se opakují.
Poslední dvě kapitoly nastínily, jak čarodějové přistupují k nekonečnu. Nekonečno je vlastně opakování.
Opakování je důležité, protože pomáhá čarodějům popsat složitější problémy. Navíc je kouzelná hůlka v opakování vážně dobrá. Jen je potřeba dát pozor, aby čaroděj stál nohama na zemi a k nekonečnu přistupoval pragmaticky – pokud chce od kouzelné hůlky výsledek vykonání kouzelných vět dostat, musí zajistit, že opakování jednou skončí.

Občas může neprogramátor zaslechnout čaroděje říkat slova, která sice nejsou kouzelná, ale stejně jim nerozumí. Občas jsou podobná slovům, které zná, a občas samotná slova dávají smysl, ale sousloví už ne.
Imperativní programování je založené na příkazech. Programátor říká počítači, co přesně má počítač vykonat. Příkazy mohou změnit stav vykonávaného programu (a světa obecně). Tomu, když se to stane, se říká vedlejší jev (side effect).
Procedurální programování je imperativní; vylepšuje strukturu zdrojového kódu tím, že příkazy rozděluje na menší části, které pojmenuje. Pojmenované části mohou být součástí jiných pojmenovaných částí a je možné je vykonávat znovu a znovu.
Objektově orientované programování (OOP) je impeprativní; vylepšuje strukturu zdrojového kódu tím, že schovává příkazy a části stavu programu do objektů. Tím vytváří hierarchii. Objekty mezi sebou komunikují přes rozhraní (interface, API), které sestává z dvou částí: (1) metody, které se na objekt volají a (2) parametry (argumenty), které se metodám předávají. Objekty v programu často představují zjednodušenou verzi objektů reálného světa a mohou obsahovat další objekty.
Deklarativní programování je založené na vztazích. Programátor říká počítači co s čím souvisí a jak.
Funkcionální programování je deklarativní; konkretizuje jej na matematické funkce. Matematická funkce nemůže nic změnit, protože jen popisuje vztah. Říkáme, že je to čistá funkce (pure function).
Logické programování je deklarativní; programátor popíše logické vztahy a nechá počítač, aby odpověděl na jeho otázku.
Rekurze, iterace i cyklus souvisí s opakováním.
Rekurze je, když kouzelná hůlka vykonává kouzelnou větu, ve které potřebuje vykonat jinou kouzelnou větu začínající stejným kouzelným slovesem.
Iterace je, když kouzelná hůlka opakuje kouzelné věty, ve kterých se mění informace ukryté v některých kouzelných podstatných jménech.
Cyklus je, když kouzelná hůlka opakuje kouzelné věty, dokud jedna z těch kouzelných vět platí.
Funkce vyššího řádu (higher order function) jsou funkce, které přijímají funkce jako argumenty a/nebo je funkce jejich návratová hodnota. Jinými slovy – kouzelná věta je vyššího řádu, když kromě prvního kouzelného slovesa je nějaké další slovo kouzelné věty také kouzelné sloveso a/nebo je kouzelné sloveso výsledek vykonání kouzelné věty.
Uzávěr (closure) je, když si funkce pamatuje a použije informaci dostupnou při definici funkce, která není argument funkce.
Anonymní (lambda) funkce je funkce, která nemá jméno.
Abstrakce je, když se více problémů dá vyřešit jedním způsobem. To znamená, že ty problémy mají něco společného. Liší se pak v konkrétních detailech.
Co třeba účastnící zájezdu? Který je nejmladší? A který bude první v abecedním seznamu? To společné je, že je potřeba účastníky seřadit. To konkrétní je podle čeho – datum narození nebo jméno.

Z neprogramátora je teď skoroprogramátor. Skoro proto, že řemeslo programátorů nejde popsat v jedné kapitole o Dopisu pro kouzelnou hůlku. Podle mě žádné řemeslo nejde popsat textem, jakkoli dlouhým. Skoro proto, že na rozdíl od neprogramátora ví, jak vést Dialog s kouzelnou hůlkou. Zná tedy základní syntax a sémantiku programovacího jazyka Racket. Skoro proto, že i když zná Nekonečně kouzelné jazykolamy, nejspíš ještě chvíli potrvá, než pochopí důsledky a jak je využít.
Neprogramátor aspiruje být první částí spirály k pochopení programování, takže skoroprogramátor je více než dobrý výsledek.